Когда мы чертим график функции, важно определить интервалы выпуклости и точки перегиба. Они, наряду с промежутками убывания и возрастания, нужны нам для четкого представления функции в графическом виде.
Понимание этой темы требует знания того, что такое производная функции и как ее вычислить до некоторого порядка, а также умения решать разные виды неравенств.
В начале статьи определяются основные понятия. Потом мы покажем, какая связь существует между направлением выпуклости и значением второй производной на определенном интервале. Далее мы укажем условия, в которых можно определить точки перегиба графика. Все рассуждения будут проиллюстрированы примерами решений задач.
Yandex.RTB R-A-339285-1 Определение 1
По направлению вниз на некотором интервале в том случае, когда ее график располагается не ниже касательной к нему в любой точке этого интервала.
Определение 2
Дифференцируемая функция является выпуклой по направлению вверх на некотором интервале в том случае, если график данной функции располагается не выше касательной к нему в любой точке этого интервала.
Выпуклую вниз функцию можно иначе назвать вогнутой. Оба определения наглядно показаны на графике ниже:
Определение 3
Точка перегиба функции – это точка M (x 0 ; f (x 0)) , в которой существует касательная к графику функции, при условии существования производной в окрестности точки x 0 , где с левой и правой стороны график функции принимает разные направления выпуклости.
Проще говоря, точка перегиба – это место на графике, в котором есть касательная, и направление выпуклости графика при прохождении через это место будет менять направление выпуклости. Если вы не помните, при каких условиях возможно существование вертикальной и невертикальной касательной, советуем повторить раздел о касательной графика функции в точке.
Ниже указан график функции, имеющей несколько точек перегиба, которые выделены красным. Уточним, что наличие точек перегиба не является обязательным. На графике одной функции их может быть одна, две, несколько, бесконечно много или ни одной.
В этом пункте мы расскажем о теореме, с помощью которой можно определить промежутки выпуклости на графике конкретной функции.
Определение 4
График функции будет иметь выпуклость по направлению вниз или вверх в том случае, если у соответствующей ему функции y = f (x) будет вторая конечная производная на указанном интервале x при условии, что неравенство f "" (x) ≥ 0 ∀ x ∈ X (f "" (x) ≤ 0 ∀ x ∈ X) будет верным.
Используя данную теорему, можно найти промежутки вогнутости и выпуклости на любом графике функции. Для этого нужно просто решить неравенства f "" (x) ≥ 0 и f "" (x) ≤ 0 на области определения соответствующей функции.
Уточним, что те точки, в которых вторая производная не существует, но функция y = f (x) определена, будут включаться в интервалы выпуклости и вогнутости.
Посмотрим на примере конкретной задачи, как правильно применять эту теорему.
Пример 1
Условие: дана функция y = x 3 6 - x 2 + 3 x - 1 . Определите, на каких промежутках ее график будет иметь выпуклости и вогнутости.
Решение
Областью определения данной функции является все множество действительных чисел. Начнем с вычисления второй производной.
y " = x 3 6 - x 2 + 3 x - 1 " = x 2 2 - 2 x + 3 ⇒ y " " = x 2 2 - 2 x + 3 = x - 2
Мы видим, что область определения второй производной совпала с областью самой функции Значит, для выявления интервалов выпуклостей нам надо решить неравенства f "" (x) ≥ 0 и f "" (x) ≤ 0 .
y "" ≥ 0 ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 y "" ≤ 0 ⇔ x - 2 ≤ 0 ⇔ x ≤ 2
Мы получили, что график заданной функции будет иметь вогнутость на отрезке [ 2 ; + ∞) и выпуклость на отрезке (- ∞ ; 2 ] .
Для наглядности изобразим график функции и отметим на нем выпуклую часть синим, а вогнутую – красным цветом.
Ответ: график заданной функции будет иметь вогнутость на отрезке [ 2 ; + ∞) и выпуклость на отрезке (- ∞ ; 2 ] .
А что же делать в случае, если область определения второй производной не совпадает с областью определения функции? Здесь нам пригодится замечание, сделанное выше: те точки, где конечная вторая производная не существует, мы тоже будем включать в отрезки вогнутости и выпуклости.
Пример 2
Условие: дана функция y = 8 x x - 1 . Определите, в каких промежутках ее график будет иметь вогнутость, а в каких – выпуклость.
Решение
Для начала выясним область определения функции.
x ≥ 0 x - 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [ 0 ; 1) ∪ (1 ; + ∞)
Теперь вычисляем вторую производную:
y " = 8 x x - 1 " = 8 · 1 2 x · (x - 1) - x · 1 (x - 1) 2 = - 4 · x + 1 x · (x - 1) 2 y "" = - 4 · x + 1 x · (x - 1) 2 " = - 4 · 1 · x · x - 1 2 - (x + 1) · x · x - 1 2 " x · (x - 1) 4 = = - 4 · 1 · x · x - 1 2 - x + 1 · 1 2 x · (x - 1) 2 + x · 2 (x - 1) x · x - 1 4 = = 2 · 3 x 2 + 6 x - 1 x 3 2 · (x - 1) 3
Область определения второй производной – это множество x ∈ (0 ; 1) ∪ (1 ; + ∞) . Мы видим, что x , равный нулю, будет принадлежать области определения исходной функции, но не области определения второй производной. Эту точку нужно обязательно включить в отрезок вогнутости или выпуклости.
После этого нам надо решить неравенства f "" (x) ≥ 0 и f "" (x) ≤ 0 на области определения заданной функции. Используем для этого метод интервалов: при x = - 1 - 2 3 3 ≈ - 2 , 1547 или x = - 1 + 2 3 3 ≈ 0 , 1547 числитель 2 · (3 x 2 + 6 x - 1) x 2 3 · x - 1 3 обращается в 0 , а знаменатель равен 0 при x , равном нулю или единице.
Нанесем получившиеся точки на график и определим знак выражения на всех интервалах, которые войдут в область определения исходной функции. На графике эта область обозначена штриховкой. Если значение положительно, отмечаем интервал плюсом, если отрицательно, то минусом.
Следовательно,
f "" (x) ≥ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) , а f "" (x) ≤ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ [ - 1 + 2 3 3 ; 1)
Включаем ранее отмеченную точку x = 0 и получаем нужный ответ. График исходной функции будет иметь выпуклость по направлению вниз при 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) , и вверх – при x ∈ [ - 1 + 2 3 3 ; 1) .
Изобразим график, отметив на нем выпуклую часть синим, а вогнутую красным цветом. Вертикальная асимптота отмечена черным пунктиром.
Ответ: График исходной функции будет иметь выпуклость по направлению вниз при 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) , и вверх – при x ∈ [ - 1 + 2 3 3 ; 1) .
Условия перегиба графика функции
Начнем с формулировки необходимого условия перегиба графика некоторой функции.
Определение 5
Допустим, что у нас есть функция y = f (x) , график которой имеет точку перегиба. При x = x 0 у него есть непрерывная вторая производная, следовательно, будет выполняться равенство f "" (x 0) = 0 .
Учитывая данное условие, нам следует поискать точки перегиба среди тех, в которых вторая производная будет обращаться в 0 . Это условие не будет достаточным: не все такие точки нам подойдут.
Также обратите внимание, что, согласно общему определению, нам нужна будет касательная прямая, вертикальная или невертикальная. На практике это означает, что для нахождения точек перегиба следует взять те, в которых вторая производная данной функции обращается в 0 . Следовательно, чтобы найти абсциссы точек перегиба, нам нужно взять все x 0 из области определения функции, где lim x → x 0 - 0 f " (x) = ∞ и lim x → x 0 + 0 f " (x) = ∞ . Чаще всего это такие точки, в которых знаменатель первой производной обращается в 0 .
Первое достаточное условие существования точки перегиба графика функции
Мы нашли все значения x 0 , которые можно взять в качестве абсцисс точек перегиба. После этого нам нужно применить первое достаточное условие перегиба.
Определение 6
Допустим, что у нас есть функция y = f (x) , которая является непрерывной в точке M (x 0 ; f (x 0)) . При этом она имеет на этой точке касательную, а сама функция имеет вторую производную в окрестности этой точки x 0 . В таком случае если с левой и правой стороны вторая производная приобретает противоположные знаки, то данную точку можно считать точкой перегиба.
Мы видим, что данное условие не требует, что в этой точке непременно существовала вторая производная, достаточно ее наличия в окрестности точки x 0 .
Все сказанное выше удобно представить в виде последовательности действий.
- Для начала нужно найти все абсциссы x 0 возможных точек перегиба, где f "" (x 0) = 0 , lim x → x 0 - 0 f " (x) = ∞ , lim x → x 0 + 0 f " (x) = ∞ .
- Выясним, в каких точках производная будет менять знак. Эти значения и есть абсциссы точек перегиба, а точки M (x 0 ; f (x 0)) , соответствующие им, – это сами точки перегиба.
Для наглядности разберем две задачи.
Пример 3
Условие: дана функция y = 1 10 · x 4 12 - x 3 6 - 3 x 2 + 2 x . Определите, где график данной функции будет иметь точки перегиба и выпуклости.
Решение
Указанная функция определена на всем множестве действительных чисел. Считаем первую производную:
y " = 1 10 · x 4 12 - x 3 6 - 3 x 2 + 2 x " = 1 10 · 4 x 3 12 - 3 x 2 6 - 6 x + 2 = = 1 10 · x 3 3 - x 2 2 - 6 x + 2
Теперь найдем область определения первой производной. Это также множество всех действительных чисел. Значит, равенства lim x → x 0 - 0 f " (x) = ∞ и lim x → x 0 + 0 f " (x) = ∞ не могут быть выполнены ни при каких значениях x 0 .
Вычисляем вторую производную:
y " " = = 1 10 · x 3 3 - x 2 2 - 6 x + 2 " = 1 10 · 3 x 2 3 - 2 x 2 - 6 = 1 10 · x 2 - x - 6
y "" = 0 ⇔ 1 10 · (x 2 - x - 6) = 0 ⇔ x 2 - x - 6 = 0 D = (- 1) 2 - 4 · 1 · (- 6) = 25 x 1 = 1 - 25 2 = - 2 , x 2 = 1 + 25 2 = 3
Мы нашли абсциссы двух вероятных точек перегиба – 2 и 3 . Все, что нам осталось сделать – это проверить, в какой точке производная изменит свой знак. Изобразим числовую ось и нанесем на нее данные точки, после чего расставим знаки второй производной на получившихся промежутках.
Дуги показывают направление выпуклости графика в каждом интервале.
Вторая производная меняет знак на противоположный (с плюса на минус) в точке с абсциссой 3 , проходя через нее слева направо, и также делает это (с минуса на плюс) в точке с абсциссой 3 . Значит, мы можем сделать вывод, что x = - 2 и x = 3 – это абсциссы точек перегиба графика функции. Им будут соответствовать точки графика - 2 ; - 4 3 и 3 ; - 15 8 .
Взглянем вновь на изображение числовой оси и получившиеся знаки на интервалах, чтобы сделать выводы о местах вогнутости и выпуклости. Получается, что выпуклость будет расположена на отрезке - 2 ; 3 , а вогнутость на отрезках (- ∞ ; - 2 ] и [ 3 ; + ∞) .
Решение задачи наглядно изображено на графике: синий цвет – выпуклости, красный – вогнутость, черный цвет означает точки перегиба.
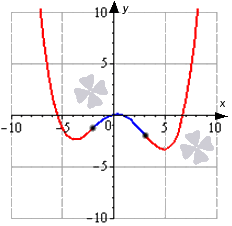
Ответ: выпуклость будет расположена на отрезке - 2 ; 3 , а вогнутость на отрезках (- ∞ ; - 2 ] и [ 3 ; + ∞) .
Пример 4
Условие: вычислите абсциссы всех точек перегиба графика функции y = 1 8 · x 2 + 3 x + 2 · x - 3 3 5 .
Решение
Область определения заданной функции – множество всех действительных чисел. Вычисляем производную:
y " = 1 8 · (x 2 + 3 x + 2) · x - 3 3 5 " = = 1 8 · x 2 + 3 x + 2 " · (x - 3) 3 5 + (x 2 + 3 x + 2) · x - 3 3 5 " = = 1 8 · 2 x + 3 · (x - 3) 3 5 + (x 2 + 3 x + 2) · 3 5 · x - 3 - 2 5 = 13 x 2 - 6 x - 39 40 · (x - 3) 2 5
В отличие от функции, ее первая производная не будет определена при значении x , равном 3 , но:
lim x → 3 - 0 y " (x) = 13 · (3 - 0) 2 - 6 · (3 - 0) - 39 40 · 3 - 0 - 3 2 5 = + ∞ lim x → 3 + 0 y " (x) = 13 · (3 + 0) 2 - 6 · (3 + 0) - 39 40 · 3 + 0 - 3 2 5 = + ∞
Это значит, что через данную точку будет проходить вертикальная касательная к графику. Следовательно, 3 может быть абсциссой точки перегиба.
Вычисляем вторую производную. Также находим область ее определения и точки, в которых она обращается в 0:
y "" = 13 x 2 - 6 x - 39 40 · x - 3 2 5 " = = 1 40 · 13 x 2 - 6 x - 39 " · (x - 3) 2 5 - 13 x 2 - 6 x - 39 · x - 3 2 5 " (x - 3) 4 5 = = 1 25 · 13 x 2 - 51 x + 21 (x - 3) 7 5 , x ∈ (- ∞ ; 3) ∪ (3 ; + ∞) y "" (x) = 0 ⇔ 13 x 2 - 51 x + 21 = 0 D = (- 51) 2 - 4 · 13 · 21 = 1509 x 1 = 51 + 1509 26 ≈ 3 , 4556 , x 2 = 51 - 1509 26 ≈ 0 , 4675
У нас получились еще две возможные точки перегиба. Нанесем их все на числовую прямую и разметим получившиеся интервалы знаками:
Перемена знака будет происходить при прохождении через каждую указанную точку, значит, они все являются точками перегиба.
Ответ: Изобразим график функции, отметив вогнутости красным, выпуклости синим и точки перегиба – черным:
Зная первое достаточное условие перегиба, мы можем определить нужные точки, в которых не обязательно наличие второй производной. Исходя из этого, первое условие можно считать наиболее универсальным и пригодным для решения разных типов задач.
Отметим, что существует еще два условия перегиба, однако их можно применять только тогда, когда в указанной точке есть конечная производная.
Если мы имеем f "" (x 0) = 0 и f """ (x 0) ≠ 0 , то x 0 будет абсциссой точки перегиба графика y = f (x) .
Пример 5
Условие: задана функция y = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5 . Определите, будет ли график функции иметь перегиб в точке 3 ; 4 5 .
Решение
Первое, что нужно сделать, – это убедиться в том, что данная точка вообще будет принадлежать графику этой функции.
y (3) = 1 60 · 3 3 - 3 20 · 3 2 - 2 5 = 27 60 - 27 20 + 21 10 - 2 5 = 9 - 27 + 42 - 8 20 = 4 5
Заданная функция определена для всех аргументов, являющихся действительными числами. Вычислим первую и вторую производные:
y " = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5 " = 1 20 x 2 - 3 10 x + 7 10 y "" = 1 20 x 2 - 3 10 x + 7 10 " = 1 10 x - 3 10 = 1 10 (x - 3)
Мы получили, что вторая производная будет обращаться в 0 , если x будет равен 0 . Значит, необходимое условие перегиба для этой точки будет выполнено. Теперь используем второе условие: найдем третью производную и выясним, будет ли она обращаться в 0 при 3:
y " " " = 1 10 (x - 3) " = 1 10
Третья производная не будет обращаться в нуль ни при одном значении x. Поэтому можно заключить, что данная точка будет точкой перегиба графика функции.
Ответ: Покажем решение на иллюстрации:
Допустим, что f " (x 0) = 0 , f "" (x 0) = 0 , . . . , f (n) (x 0) = 0 и f (n + 1) (x 0) ≠ 0 .В таком случае при четном n мы получим, что x 0 – это абсцисса точки перегиба графика y = f (x) .
Пример 6
Условие: дана функция y = (x - 3) 5 + 1 . Вычислите точки перегиба ее графика.
Решение
Данная функция является определенной на всем множестве действительных чисел. Вычисляем производную: y " = ((x - 3) 5 + 1) " = 5 · x - 3 4 . Поскольку она тоже будет определена для всех действительных значений аргумента, то в любой точке ее графике будет существовать невертикальная касательная.
Теперь вычислим, при каких значениях вторая производная будет обращаться в 0:
y "" = 5 · (x - 3) 4 " = 20 · x - 3 3 y "" = 0 ⇔ x - 3 = 0 ⇔ x = 3
Мы получили, что при x = 3 график функции может иметь точку перегиба. Используем третье условие, чтобы подтвердить это:
y " " " = 20 · (x - 3) 3 " = 60 · x - 3 2 , y " " " (3) = 60 · 3 - 3 2 = 0 y (4) = 60 · (x - 3) 2 " = 120 · (x - 3) , y (4) (3) = 120 · (3 - 3) = 0 y (5) = 120 · (x - 3) " = 120 , y (5) (3) = 120 ≠ 0
Имеем n = 4 по третьему достаточному условию. Это четное число, значит, x = 3 будет абсциссой точки перегиба и ей соответствует точка графика функции (3 ; 1) .
Ответ: Вот график данной функции с отмеченными выпуклостями, вогнутостями и точкой перегиба:
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Осталось рассмотреть выпуклость, вогнутость и перегибы графика . Начнём с так полюбившихся посетителям сайта физических упражнений. Пожалуйста, встаньте и наклонитесь вперёд либо назад. Это выпуклость. Теперь вытяните руки перед собой ладонями вверх и представьте, что держите на груди большое бревно… …ну, если не нравится бревно, пусть будет ещё что/кто-нибудь =) Это вогнутость. В ряде источников встречаются синонимичные термины выпуклость вверх и выпуклость вниз , но я сторонник коротких названий.
! Внимание
: некоторые авторы определяют выпуклость и вогнутость с точностью до наоборот
. Это математически и логически тоже верно, но зачастую совершенно некорректно с содержательной точки зрения, в том числе на уровне нашего обывательского понимания терминов. Так, например, двояковыпуклой линзой называют линзу именно «с бугорками», но никак не со «вдавленностями» (двояковогнутость).
А, скажем, «вогнутая» кровать – она всё-таки явно не «торчит вверх» =) (однако если под неё залезть, то речь уже зайдёт о выпуклости;=)) Я придерживаюсь подхода, который соответствует естественным человеческим ассоциациям.
Формальное определение выпуклости и вогнутости графика достаточно труднО для чайника, поэтому ограничимся геометрической интерпретацией понятия на конкретных примерах. Рассмотрим график функции , которая непрерывна
на всей числовой прямой:
Его легко построить с помощью геометрических преобразований
, и, наверное, многие читатели в курсе, как он получен из кубической параболы.
Назовём хордой отрезок, соединяющий две различные точки графика.
График функции является выпуклым на некотором интервале, если он расположен не ниже любой хорды данного интервала. Подопытная линия выпукла на , и, очевидно, что здесь любая часть графика расположена НАД своей хордой . Иллюстрируя определение, я провёл три чёрных отрезка.
График функции являются вогнутым на интервале, если он расположен не выше любой хорды этого интервала. В рассматриваемом примере пациент вогнут на промежутке . Пара коричневых отрезков убедительно демонстрирует, что тут и любой кусок графика расположен ПОД своей хордой .
Точка графика, в которой он меняет выпуклость на вогнутость или вогнутость на выпуклость, называется точкой перегиба . У нас она в единственном экземпляре (первый случай), причём, на практике под точкой перегиба можно подразумевать как зелёную точку , принадлежащую самой линии, так и «иксовое» значение .
ВАЖНО! Перегибы графика следует изображать аккуратно и очень плавно . Недопустимы всевозможные «неровности» и «шероховатости». Дело за небольшой тренировкой.
Второй подход к определению выпуклости/вогнутости в теории даётся через касательные:
Выпуклый на интервале график расположен не выше касательной, проведённой к нему в произвольной точке данного интервала. Вогнутый же на интервале график – не ниже любой касательной на этом интервале.
Гипербола вогнута на интервале и выпукла на :
При переходе через начало координат вогнутость меняется на выпуклость, однако точку НЕ СЧИТАЮТ
точкой перегиба, так как функция не определена
в ней.
Более строгие утверждения и теоремы по теме можно найти в учебнике, а мы переходим к насыщенной практической части:
Как найти интервалы выпуклости, интервалы вогнутости
и точки перегиба графика?
Материал прост, трафаретен и структурно повторяет исследование функции на экстремум .
Выпуклость/вогнутость графика характеризует вторая производная функции .
Пусть функция дважды дифференцируема на некотором интервале. Тогда:
– если вторая производная на интервале, то график функции является выпуклым на данном интервале;
– если вторая производная на интервале, то график функции является вогнутым на данном интервале.
На счёт знаков второй производной по просторам учебных заведений гуляет доисторическая ассоциация: «–» показывает, что «в график функции нельзя налить воду» (выпуклость),
а «+» – «даёт такую возможность» (вогнутость).
Необходимое условие перегиба
Если в точке есть перегиб графика функции
, то:
либо значения не существует
(разберём, читайте!)
.
Данная фраза подразумевает, что функция непрерывна в точке и в случае – дважды дифференцируема в некоторой её окрестности.
Необходимость условия говорит о том, что обратное справедливо не всегда. То есть из равенства (либо небытия значения ) ещё не следует существования перегиба графика функции в точке . Но и в той, и в другой ситуации называют критической точкой второй производной .
Достаточное условие перегиба
Если вторая производная при переходе через точку меняет знак, то в данной точке существует перегиб графика функции .
Точек перегиба (встретился уже пример) может не быть вовсе, и в этом смысле показательны некоторые элементарные образцы. Проанализируем вторую производную функции :
Получена положительная функция-константа, то есть для любого значения «икс» . Факты, лежащие на поверхности: парабола вогнута на всей области определения , точки перегиба отсутствуют. Легко заметить, что отрицательный коэффициент при «переворачивает» параболу и делает её выпуклой (о чём нам сообщит вторая производная – отрицательная функция-константа).
Экспоненциальная функция также вогнута на :
для любого значения «икс».
Точек перегиба у графика , разумеется, нет.
Исследуем на выпуклость/вогнутость график логарифмической функции :
Таким образом, ветка логарифма является выпуклой на интервале . Вторая производная определена и на промежутке , но рассматривать его НЕЛЬЗЯ , поскольку данный интервал не входит в область определения функции . Требование очевидно – коль скоро там нет графика логарифма, то ни о какой выпуклости/вогнутости/перегибах речи, естественно, не заходит.
Как видите, всё действительно очень напоминает историю с возрастанием, убыванием и экстремумами функции . Похож и сам алгоритм исследования графика функции на выпуклость, вогнутость и наличие перегибов :
2) Разыскиваем критические значения. Для этого берём вторую производную и решаем уравнение . Точки, в которых не существует 2-й производной, но которые входят в область определения самой функции – тоже считаются критическими!
3) Отмечаем на числовой прямой все найденные точки разрыва и критические точки (ни тех, ни других может не оказаться – тогда чертить ничего не надо (как и в слишком простом случае), достаточно ограничиться письменным комментарием) . Методом интервалов определяем знаки на полученных интервалах. Как только что пояснялось, рассматривать следует только те промежутки, которые входят в область определения функции . Делаем выводы о выпуклости/вогнутости и точках перегиба графика функции . Даём ответ.
Попытайтесь устно применить алгоритм для функций 
. Во втором случае, кстати, пример, когда в критической точке не существует перегиба графика. Впрочем, начнём с ненамного более сложных заданий:
Пример 1
Решение
:
1) Функция определена и непрерывна на всей числовой прямой. Очень хорошо.
2) Найдём вторую производную. Можно предварительно выполнить возведение в куб, но значительно выгоднее использовать правило дифференцирование сложной функции
:
Заметьте, что 
, а значит, функция является неубывающей
. Хоть это и не относится к заданию, но на такие факты всегда желательно обращать внимание.
Найдём критические точки второй производной:
– критическая точка
3) Проверим выполнение достаточного условия перегиба. Определим знаки второй производной на полученных интервалах .
Внимание! Сейчас работаем со второй производной (а не с функцией!)
В результате получена одна критическая точка: .
3) Отметим на числовой прямой две точки разрыва, критическую точку и определим знаки второй производной на полученных интервалах:
Напоминаю важный приём метода интервалов
, позволяющий значительно ускорить решение. Вторая производная 
получилась весьма громоздкой, поэтому не обязательно рассчитывать её значения, достаточно сделать «прикидку» на каждом интервале. Выберем, например, точку , принадлежащее левому промежутку,
и выполним подстановку:
Теперь анализируем множители:
Два «минуса» и «плюс» дают «плюс», поэтому , а значит, вторая производная положительна и на всём интервале .
Закомментированные действия несложно выполнить устно. Кроме того, множитель выгодно игнорировать вообще – он положителен при любом «икс» и не оказывает влияния на знаки нашей второй производной.
Итак, какую информацию нам предоставила ?
Ответ
: график функции является вогнутым на 
и выпуклым на 
. В начале координат (ясно, что )
существует перегиб графика.
При переходе через точки вторая производная тоже меняет знак, но они не считаются точками перегиба, так как функция терпит в них бесконечные разрывы .
В разобранном примере первая производная 
сообщает нам о росте функции на всей области определения
. Всегда бы такая халява =) Кроме того, очевидно наличие трёх асимптот
. Данных получено много, что позволяет с высокой степенью достоверности представить внешний вид графика. До кучи, функция ещё и нечётная. Исходя из установленных фактов, попытайтесь выполнить набросок на черновике. Картинка в конце урока.
Задание для самостоятельного решения:
Пример 6
Исследовать график функции на выпуклость, вогнутость и найти точки перегиба графика, если они существует.
Чертежа в образце нет, но гипотезу выдвинуть не возбраняется;)
Шлифуем материал, не нумеруя пункты алгоритма:
Пример 7
Исследовать график функции на выпуклость, вогнутость и найти точки перегиба, если они существует.
Решение : функция терпит бесконечный разрыв в точке .
У нас как обычно, всё отлично:
Производные не самые трудные, главное быть внимательным с их «причёской».
В наведённом марафете обнаруживаются две критические точки второй производной:
Определим знаки на полученных интервалах:
В точке существует перегиб графика, найдём ординату точки:
При переходе через точку вторая производная не меняет знак, следовательно, в ней НЕТ перегиба графика.
Ответ
: интервалы выпуклости: 
; интервал вогнутости: ; точка перегиба: .
Рассмотрим заключительные примеры с дополнительными примочками:
Пример 8
Найти интервалы выпуклости, вогнутости и точки перегиба графика
Решение
: с нахождением области определения
особых проблем не возникает:
, при этом в точках функция терпит разрывы.
Идём проторенной дорогой:
– критическая точка.
Определим знаки , при этом рассматриваем интервалы только из области определения функции
:
В точке существует перегиб графика, вычислим ординату:
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word . Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе .
Правила ввода функций :
Направление выпуклости графика функции. Точки перегиба
Определение : Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.Определение
: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
Определение : Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x) , характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение:
Точка графика функции y=f(x) , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x) , в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x) .
- Найти критические точки II рода функции y=f(x) , т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x) . Если при этом критическая точка x 0 разделяет промежутки выпуклости противоположных направлений, то x 0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1
. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x 2 –x 3 .
Решение: Находим f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0 . x=2 .
f(2) = 6*2 2 – 2 3 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞) ; функция выпукла вниз при x∈(-∞; 2) ; точка перегиба (2;16) .
Пример 2 . Имеет ли точки перегиба функция: f(x)=x 3 -6x 2 +2x-1
Пример 3 . Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x 3 -6x 2 +12x+4
