Xaos фракталы. Золотая пропорция, фракталы и хаос в связи с некоторыми представлениями о мироздании. От хаоса

ФРАКТАЛЫ И ТЕОРИЯ ХАОСА

Иван Тугой

РАЗДЕЛ 1: ОБЩИЕ СВЕДЕНИЯ

ФРАКТАЛЫ И МИР ВОКРУГ НАС

Фракталы - уникальные объекты, порожденные непредсказуемыми движениями хаотического мира. Их находят в местах таких малых, как клеточная мембрана и таких огромных, как Солнечная система.

Разветвления трубочек трахей, листья на деревьях, вены в руке, река, бурлящая и изгибающаяся, рынок ценных бумаг - это все фракталы. От представителей древних цивилизаций до Майкла Джексона, ученые, математики и артисты, как и все остальные обитатели этой планеты, были зачарованы фракталами и применяли из в своей работе.

Программисты и специалисты в области компьютерной техники так же без ума от фракталов, так как фракталы бесконечной сложности и красоты могут быть сгенерированы простыми формулами на простых домашних компьютерах. Открытие фракталов было открытием новой эстетики искусства, науки и математики, а так же революцией в человеческом восприятии мира.

ЧТО ЖЕ ТАКОЕ ФРАКТАЛЫ НА САМОМ ДЕЛЕ?

Слово “Фрактал” - это что-то, о чем много людей говорит в наши дни, от физиков до учеников средней школы. Оно появляется на обложках многих учебников математики, научных журналов и коробках с компьютерным программным обеспечением. Цветные картинки фракталов сегодня можно найти везде: от открыток до футболок. За последние два десятка лет количество производимых в месяц единиц продукции, связанной с фракталами, увеличилось от нескольких десятков до многих тысяч!

Итак, что это за цветные формы, которые мы видим повсюду вокруг? Говоря простым языком, фрактал - это геометрическая фигура, определенная часть которой повторяется снова и снова, изменяясь в размерах. Отсюда следует принцип самоподобия. Все фракталы подобны самим себе, то есть они похожи на всех уровнях. Существует много типов фракталов, причем здесь описываются довольно большое их количество.

Однако фракталы - не просто сложные фигуры, сгенерированные компьютерами. Все, что кажется случайным и неправильным может быть фракталом. Теоретически, можно сказать, что все что существует в реальном мире является фракталом, будь то облако или маленькая молекула кислорода.

НАСКОЛЬКО ХАОТИЧЕН ХАОС?

Фракталы всегда ассоциируются со словом хаос. Я лично, определил бы фракталы, как частички хаоса. Фракталы проявляют хаотическое поведение, благодаря которому они кажутся такими беспорядочными и случайными. Но если взглянуть достаточно близко, можно увидеть много аспектов самоподобия внутри фрактала. Например, посмотрите на дерево, затем выберите определенную ветку и изучите ее поближе. Теперь выберите связку из нескольких листьев. Для ученых, занимающихся фракталами (которых иногда называют хаологами), все эти три объекта представляются идентичными.

Слово хаос наводит большинство людей на мысли о чем-то беспорядочном и непредсказуемом. На самом деле, это не совсем так. Итак насколько хаотичен хаос? Ответ таков, что хаос, в действительности, достаточно упорядочен и подчиняется определенным законам. Проблема состоит в том, что отыскание этих законов может быть очень сложным. Цель изучения хаоса и фракталов - предсказать закономерность в системах, которые могут казаться непредсказуемыми и абсолютно хаотическими.

Система - это набор вещей, или область изучения, причем некоторые из обычных систем, которые хаологи любят изучать включают облачные образования, погода, движение водных потоков, миграции животных, и множество других аспектов из жизни матери природы. Так что, в конце концов, может быть, весь мир вокруг нас фрактален!

ГЕОМЕТРИЯ 21 ВЕКА

Для многих хаологов, изучение хаоса и фракталов не просто новая область познания, которая объединяет математику, теоретическую физику, искусство и компьютерные технологии - это революция. Это открытие нового типа геометрии, той геометрии, которая описывает мир вокруг нас и которую можно увидеть не только в учебниках, но и в природе и везде в безграничной вселенной.

Пионером в этой новой области познания, которого многие называют отцом фракталов был Франко-Американский математик Профессор Бенуа Б. Мандельброт (Benoit B. Mandelbrot). В середине 1960х после десятилетий обучения и научной деятельности, Мандельброт разработал то, что он назвал фрактальная геометрия или геометрия природы (об этом он написал свой бестселлер - Фрактальная геометрия природы). Целью фрактальной геометрии был анализ сломанных, морщинистых и нечетких форм. Мандельброт использовал слово фрактал, потому что это предполагало осколочность и фракционность этих форм.

Сегодня Мандельброт и другие ученые, такие как Клиффорд А. Пикковер (Clifford A. Pickover), Джеймс Глейк (James Gleick) или Г. О. Пейтген (H.O. Peitgen) пытаются расширить область фрактальной геометрии так, чтобы она могла быть применена практически ко всему в мире, от предсказания цен на рынке ценных бумаг до совершения новых открытий в теоретической физике.

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ФРАКТАЛОВ

Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Вот несколько примеров:

КОМПЬЮТЕРНЫЕ СИСТЕМЫ

Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

МЕХАНИКА ЖИДКОСТЕЙ

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков.

При помощи фракталов также можно смоделировать языки пламени.

Пористые материалы хорошо представляются в фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.

ТЕЛЕКОММУНИКАЦИИ

Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.

ФИЗИКА ПОВЕРХНОСТЕЙ

Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.

МЕДИЦИНА

Биосенсорные взаимодействия

Биения сердца

БИОЛОГИЯ

Моделирование хаотических процессов, в частности при описании моделей популяций.

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ: СПРЯТАННЫЕ ИЗМЕРЕНИЯ

Одной из идей, выросших из открытия фрактальной геометрии была идея нецелых значений для количества измерений в пространстве. Конечно, мы не можем осознать четырехмерные вещи, хотя Lucky Tesseract и активно работает в этом направлении. Мандельброт назвал нецелые измерения такие как 2.76 фрактальными измерениями. Обыкновенная евклидова геометрия утверждает, что пространство ровное и плоское. Свойства такого пространства такого пространства задают точки, линии, углы, треугольники, кубы, сферы, тетраэдры и т. д.

Мандельброт верил, что действительный ландшафт пространства не ровный и что в нашем мире нет ничего, что было бы совершенно плоским, круглым, то есть все фрактально. Следовательно объект, имеющий точно 3 измерения невозможен. Вот почему концепция фрактального измерения была нужна для измерения степени неровности вещей.

Например посмотрите на лист бумаги (предположим, что он двумерный), скомканный в шар. Разве он двумерный? Нет, так как у него есть длина, ширина и высота. Но он не может быть и трехмерным, потому что он сделан из одного бесконечно тонкого листа и, к тому же, он не полностью однородный. Итак, его фрактальная размерность приблизительно равна 2.5. Но его нормальная размерность, так же называемая Евклидовой размерностью будет равна 3. Все фракталы, особенно фрактальные кривые, имеют фрактальные размерности. Мандельброт часто использовал пример того, что береговая линия Англии имеет бесконечную длину.

Попытайтесь наложить нитку на береговую линии Англии на атласе. Затем сделайте то же самое с мореходной картой. Удивительно, но величина последнего измерения будет гораздо больше. Затем поезжайте в Англию и измерьте ее береговую линию метровой полкой. Эта длина будет еще длинней. Продолжайте этот процесс до тех пор, пока у вас в руках не окажется чертежная линейка, которой вы можете измерить береговую линию частичка за частичкой, атом за атомом. Конечно идея этого непрактичного эксперимента в том, что расстояния должны быть соизмеримы по масштабу, положению и деталям. Позже Мандельброт определил, что фрактальная размерность береговой линии Англии составляет 1.25.

Многие объекты в природе (например человеческое тело) состоят из множества фракталов, смешанных друг с другом, причем каждый фрактал имеет свою размерность отличную от размерности остальных. Например, двумерная поверхность человеческой сосудистой системы изгибается, ветвится, скручивается и сжимается так, что ее фрактальная размерность равна 3.0. Но если бы она была разделена на отдельные части, фрактальная размерность артерий была бы только 2.7, тогда как бронхиальные пути в легких имели бы фрактальную размерность 1.07.

РАЗДЕЛ 2: ДЕТЕРМИНИРОВАННЫЕ ФРАКТАЛЫ

ОБЩАЯ ХАРАКТЕРИСТИКА

Первыми открытыми фракталами были т.н. детерминированные фракталы. Их отличительной чертой является свойство самоподобия, обусловленное особенностями метода их генерации.

Некоторые предпочитают называть эти фракталы классическими, геометрическими фракталами или линейными фракталами. Эти фракталы обычно формируются начиная с инициатора - фигуры, к которой применяется определенный основной рисунок. Во всех детерминированных фракталах, само-подобие проявляется на всех уровнях. Это значит, что независимо от того насколько вы приближаете фрактал, вы увидите все тот же узор. Для сложных фракталов, которые будут рассмотрены позже, это не так. Детерминистские фракталы образуются в процессе, называемом итерацией, которая применяет основной рисунок к инициатору, после чего применяет его к результату и так далее. Большинство людей итерируют детерминированные фракталы 5-7 раз чтобы получить четкую красивую картинку. Эти фракталы линейны, так как при каждой итерации, что-то убирается либо прибавляется в форме прямых линий. Ниже находятся примеры некоторых обычных детерминированных фракталов, сгенерированных на обычном компьютере простыми программами на BASIC’е.

РЕШЕТКА СЕРПИНСКОГО

Это один из фракталов, с которыми экспериментировал Мандельброт, когда разрабатывал концепции фрактальных размерностей и итераций. Треугольники, сформированные соединением средних точек большего треугольника вырезаны из главного треугольника, образовывая треугольник, с большим количеством дырочек. В этом случае инициатор - большой треугольник а шаблон - операция вырезания треугольников, подобных большему. Так же можно получить и трехмерную версию треугольника, используя обыкновенный тетраэдр и вырезая маленькие тетраэдры. Размерность такого фрактала ln3/ln2 = 1.584962501.

Чтобы получить ковер Серпинского, возьмем квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. В конце концов образуется плоская фрактальная сетка, не имеющая площади, но с бесконечными связями. В своей пространственной форме, губка Серпинского преобразуется в систему сквозных форм, в которой каждый сквозной элемент постоянно заменяется себе подобным. Эта структура очень похожа на разрез костной ткани. Когда-нибудь такие повторяющиеся структуры станут элементом строительных конструкций. Их статика и динамика, считает Мандельброт, заслуживает пристального изучения.

ФРАКТАЛ СЕРПИНСКОГО

Не перепутайте этот фрактал с решеткой Серпинского. Это два абсолютно разных объекта. В этом фрактале, инициатор и генератор одинаковы. При каждой итерации, добавляется уменьшенная копия инициатора к каждому углу генератора и так далее. Если при создании этого фрактала произвести бесконечное число итераций, он бы занял всю плоскость, не оставив ни одной дырочки. Поэтому его фрактальная размерность ln9/ln3 = 2.0

КРИВАЯ КОХА

Кривая Коха один из самых типичных детерминированных фракталов. Она была изобретена в девятнадцатом веке немецким математиком по имени Хельге фон Кох, который, изучая работы Георга Контора и Карла Вейерштрассе, натолкнулся на описания некоторых странных кривых с необычным поведением. Инициатор - прямая линия. Генератор - равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова. В своем исследовании, Мандельброт много экспериментировал с кривыми Коха, и получил фигуры такие как Острова Коха, Кресты Коха, Снежинки Коха и даже трехмерные представления кривой Коха, используя тетраэдр и прибавляя меньшие по размерам тетраэдры к каждой его грани. Кривая Коха имеет размерность ln4/ln3 = 1.261859507.

Крест Коха - это один из вариантов кривой Коха, изобретенный Мандельбротом. Вместо отрезка прямой, он использовал в качестве инициатора квадрат или прямоугольник. Так как в этом фрактале использован та же самая идея что и в оригинальной кривой Коха, его фрактальная размерность такая же: ln4/ln3 = 1.261859507.

ФРАКТАЛ МАНДЕЛЬБРОТА

Это НЕ множество Мандельброта, которое можно достаточно часто видеть. Множество Мандельброта основано на нелинейных уравнениях и является комплексным фракталом. Это тоже вариант кривой Коха несмотря на то, что этот объект не похож на нее. Инициатор и генератор так же отличны от использованных для создания фракталов, основанных на принципе кривой Коха, но идея остается той же. Вместо того, чтобы присоединять равносторонние треугольники к отрезку кривой, квадраты присоединяются к квадрату. Благодаря тому, что этот фрактал занимает точно половину отведенного пространства при каждой итерации, он имеет простую фрактальную размерность 3/2 = 1.5

ФРАКТАЛЫ ЗВЕЗДА И СНЕЖИНКА

Оба эти объекта не являются классическими фракталами и они не были изобретены Мандельбротом или кем-либо из известных математиков. Я просто создал эти фракталы из интереса и чтобы поэкспериментировать в программировании. И инициатор и генератор здесь фигура, сформированная соединением средних точек сторон со средними точками противолежащих сторон в правильном шестиугольнике. Более того, я могу только подозревать о размерности этих фракталов.

КОЛБАСА МИНКОВСКОГО

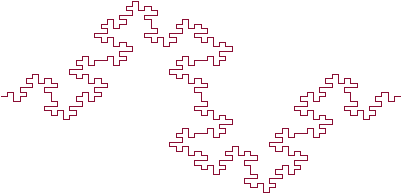
Автор этого фрактала Герман Минковский, по имени которого он и был назван. Минковский не предлагал термин колбаса для названия этого объекта. Слово кривая или просто фрактал, возможно, понравилось бы больше. И инициатор и генератор довольно сложны и составлены из ряда прямых углов и сегментов различной длины. У самого инициатора 8 частей. Фрактальная размерность колбасы Минковского - ln8/ln4 = 1.5

ФРАКТАЛ ЛАБИРИНТ

Этот фрактал еще иногда называют H-деревом. И инициатор и генератор имеют вид буквы H. На приведенном здесь примере сама H не закрашена. Вместо этого заполнены области вне фрактала, что облегчает восприятие рисунка и шаблона. Фрактальная размерность этого конкретно фрактала весьма интересна. Так как толщина H в процессе итераций уменьшается, размерность кончиков буквы H точно 2.0, но элементы между кончиками имеют другую размерность, меняющуюся от 1.3333 до 1.6667.

ПЯТИУГОЛЬНИК ДАРЕРА

Фрактал выглядит как связка пятиугольников, сжатых вместе. Фактически он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей в которых в точности равно так называемой золотой пропорции (1.618033989 или 1/(2cos72)) в качестве генератора. Эти треугольники вырезаются из середины каждого пятиугольника, в результате чего получается фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому.

Вариант этого фрактала можно получить при использовании в качестве инициатора шестиугольника. Этот фрактал называется Звезда Давида и он довольно похож на шестиугольную версию Снежинки Коха. Фрактальная размерность пятиугольника Дарера ln6/ln(1+g), где g - отношение длины большей стороны треугольника к длине меньшей. В данном случае, g - это Золотая Пропорция, так что фрактальная размерность приблизительно равна 1.86171596. Фрактальное измерение Звезды Давида ln6/ln3 или 1.630929754.

КРИВАЯ ДРАКОНА

Изобретенная итальянским математиком Джузеппе Пеано, Кривая Дракона или Взмах Дракона, как он назвал его, очень похож на колбасу Минковского. Использован более простой инициатор, а генератор тот же самый. Мандельброт назвал этот фрактал Река Двойного Дракона. Его фрактальная размерность приблизительно равна 1.5236.

КРИВАЯ ГИЛЬБЕРТА

Этот фрактал очень похож на Фрактал Лабиринт, кроме того факта что ширина буквы U, являющейся генератором не изменяется с каждой итерацией. Однако, в отличии от Фрактала Лабиринта, кривая Гильберта также называемая Отелем Гильберта, имеет одно единственное фрактальное измерение, которое точно равно 2.0, так как при бесконечном количестве итераций, он займет всю плоскость.

ФРАКТАЛ КОРОБКА

Это очень простой детерминированный фрактал, который образуется при прибавлении квадратов к вершинам других квадратов. И инициатор и генератор - квадраты. Его фрактальная размерность ln8/ln3 или 1.892789261.

РАЗДЕЛ 3: СЛОЖНЫЕ ФРАКТАЛЫ

ОБЩАЯ ХАРАКТЕРИСТИКА

Большая часть встречающихся сегодня фракталов не являются детерминированными. Они не линейны и не собранны из повторяющихся геометрических форм. Такие фракталы называются сложными.

Фактически, если вы увеличите маленькую область любого сложного фрактала а затем проделаете то же самое с маленькой областью этой области, то эти два увеличения будут значительно отличаться друг от друга. Два изображения будут очень похожи в деталях, но они не будут полностью идентичными.

Сравните, например приведенные здесь картинки множества Мандельброта, одна из которых получена при увеличении некоторой области другой. Как видно, они абсолютно не являются идентичными, хотя на обоих мы видим черный круг, от которого в разные стороны идут пылающие щупальца. Эти элементы повторяются бесконечно долго во множестве Мандельброта в уменьшающейся пропорции.

Детерминистские фракталы являются линейными, тогда как сложные фракталы таковыми не являются. Будучи нелинейными, эти фракталы генерируются тем, что Мандельброт назвал нелинейными алгебраическими уравнениями. Хороший пример - это процесс Zn+1=ZnІ + C, что является уравнением, используемым для построения множества Мандельброта и Жулии второй степени. Решение этих математических уравнений вовлекает комплексные и мнимые числа. Когда уравнение интерпретируется графически на комплексной плоскости, результатом оказывается странная фигура, в которой прямые линии переходят в кривые, появляются хотя и не без деформаций, эффекты самоподобия на различных масштабных уровнях. При этом вся картина в целом является непредсказуемой и очень хаотичной.

Как можно увидеть, смотря на картинки, сложные фракталы действительно очень сложны и их невозможно создать без помощи компьютера. Для получения красочных результатов этот компьютер должен обладать мощным математическим сопроцессором и монитором с высоким разрешением. В отличии от детерминистских фракталов, сложные фракталы не вычисляются за 5-10 итераций. Практически каждая точка на экране компьютера как отдельный фрактал. Во время математической обработки, каждая точка рассматривается как отдельный рисунок. Каждой точке соответствует определенное значение. Уравнение встраивается, применительно к каждой точке и производится, к примеру 1000 итераций. Для получения сравнительно неискаженного изображения за приемлемый для домашних компьютеров промежуток времени, для одной точки возможно проводить 250 итерации.

Большинство фракталов, которые мы видим сегодня, красиво раскрашены. Возможно фрактальные изображения получили такое большое эстетическое значение именно благодаря своим цветовым схемам. После того, как уравнение посчитано, компьютер анализирует результаты. Если результаты остаются стабильными, или колеблются вокруг определенного значения, точка обычно принимает черный цвет. Если значение на том или ином шаге стремится к бесконечности, точку закрашивают в другой цвет, может быть в синий или красный. Во время этого процесса, компьютер назначает цвета для всех скоростей движения.

Обычно, быстро движущиеся точки закрашивают в красный цвет, тогда как более медленные в желтый и так далее. Темные точки, вероятно, самые стабильные.

Сложные фракталы отличаются от детерминистских в том смысле, что они бесконечно сложные, но, при этом, могут быть сгенерированы очень простой формулой. Детерминистским фракталам не нужны формулы или уравнения. Просто возьмите чертежную бумагу и вы можете построить решето Серпинского до 3 или 4 итерации без каких-либо затруднений. Попробуйте сделать это с множеством Жулиа! Легче пойти мерить длину береговой линии Англии!

МНОЖЕСТВО МАНДЕЛЬБРОТА

Множества Мандельброта и Жулиа, вероятно, два наиболее распространенных среди сложных фракталов. Их можно найти во многих научных журналах, обложках книг, открытках, и в компьютерных хранителях экрана. Множество Мандельброта, которое было построено Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они слышат слово фрактал. Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями, генерируется простой формулой Zn+1=Zna+C, где Z и C - комплексные числа и а - положительное число.

Множество Мандельброта, которое чаще всего можно увидеть - это множество Мандельброта 2й степени, то есть а=2. Тот факт, что множество Мандельброта не только Zn+1=ZnІ+C, а фрактал, показатель в формуле которого может быть любым положительным числом ввел в заблуждение многих. На этой странице вы видите пример множества Мандельброта для различных значений показателя а.

Также популярен процесс Z=Z*tg(Z+C). Благодаря включению функции тангенса, получается множество Мандельброта, окруженное областью, напоминающей яблоко. При использовании функции косинуса, получаются эффекты воздушных пузырьков. Короче говоря, существует бесконечное количество способов настройки множества Мандельброта для получения различных красивых картинок.

МНОЖЕСТВО ЖУЛИА

Удивительно, но множества Жулиа образуются по той же самой формуле, что и множество Мандельброта. Множество Жулиа было изобретено французским математиком Гастоном Жулиа, по имени которого и было названо множество. Первый вопрос, возникающий после визуального знакомства с множествами Мандельброта и Жулиа это “если оба фрактала сгенерированы по одной формуле, почему они такие разные?” Сначала посмотрите на картинки множества Жулиа. Достаточно странно, но существуют разные типы множеств Жулиа. При рисовании фрактала с использованием различных начальных точек (чтобы начать процесс итераций), генерируются различные изображения. Это применимо только ко множеству Жулиа:

Хотя это нельзя увидеть на картинке, фрактал Мандельброта - это, на самом деле, множество фракталов Жулиа, соединенных вместе. Каждая точка (или координата) множества Мандельброта соответствует фракталу Жулиа. Множества Жулиа можно сгенерировать используя эти точки в качестве начальных значений в уравнении Z=ZІ+C. Но это не значит, что если выбрать точку на фрактале Мандельброта и увеличить ее, можно получить фрактал Жулиа. Эти две точки идентичны, но только в математическом смысле. Если взять эту точку и просчитать ее по данной формуле, можно получить фрактал Жулиа, соответствующий определенной точке фрактала Мандельброта.

РАЗДЕЛ 4: ТЕОРИЯ ХАОСА

ЧТО ТАКОЕ ТЕОРИЯ ХАОСА?

Формально, теория хаоса определяется как учение о сложных нелинейных динамических системах. Под термином сложные это и понимается, а под термином нелинейные понимается рекурсия и алгоритмы из высшей математики, и, наконец, динамические - означает непостоянные и непериодические. Таким образом, теория хаоса – это учение о постоянно изменяющихся сложных системах, основанное не математических концепциях рекурсии, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему.

НЕПРАВИЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О ТЕОРИИ ХАОСА

Широкая общественность обратила внимание на теорию хаоса благодаря таким фильмам, как Парк юрского периода, и благодаря им же, постоянно увеличивается опасение теории хаоса со стороны общества. Однако, как и в отношении любой вещи, освещаемой средствами массовой информации, в отношении теории хаоса возникло много неправильных представлений.

ТЕОРИЯ ХАОСА О БЕСПОРЯДКЕ

Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса - это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок - и даже не просто порядок, а сущность порядка.

Это правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы - наследственной непредсказуемости системы - а на унаследованном ей порядке - общем в поведении похожих систем.

Таким образом, было бы неправильным сказать, что теория хаоса о беспорядке. Чтобы пояснить это на примере, возьмем аттрактор Лоренца. Он основан на трех дифференциальных уравнениях, трех константах и трех начальных условиях.

Аттрактор представляет поведение газа в любое заданное время, и его состояние в определенный момент зависит от его состояния в моменты времени, предшествовавшие данному. Если исходные данные изменить даже на очень маленькие величины, скажем, эти величины малы настолько, что соизмеримы с колебаниями числа Авогадро (очень маленькое число порядка 10 24), проверка состояния аттрактора покажет абсолютно другие числа. Это происходит потому, что маленькие различия увеличиваются в результате рекурсии. Однако, несмотря на это, график аттрактора будет выглядеть достаточно похоже. Обе системы будут иметь абсолютно разные значения в любой заданный момент времени, но график аттрактора останется тем же самым, т.к. он выражает общее поведение системы.

Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы - в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах.

Однако согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни.

ПРИМЕНЕНИЕ ТЕОРИИ ХАОСА В РЕАЛЬНОМ МИРЕ

При появлении новых теорий, все хотят узнать что же в них хорошего. Итак что хорошего в теории хаоса?

Первое и самое важное - теория хаоса - это теория. А значит, что большая ее часть используется больше как научная основа, нежели как непосредственно применимое знание. Теория хаоса является очень хорошим средством взглянуть на события, происходящие в мире отлично от более традиционного четко детерминистического взгляда, который доминировал в науке со времен Ньютона. Зрители, которые посмотрели Парк Юрского периода, без сомнения боятся, что теория хаоса может очень сильно повлиять на человеческое восприятие мира, и, в действительности, теория хаоса полезна как средство интерпретации научных данных по-новому. Вместо традиционных X-Y графиков, ученые теперь могут интерпретировать фазово-пространственные диаграммы которые - вместо того, чтобы описывать точное положение какой-либо переменной в определенный момент времени - представляют общее поведение системы. Вместо того, чтобы смотреть на точные равенства, основанные на статистических данных, теперь мы можем взглянуть на динамические системы с поведением похожим по своей природе на статические данные - т.е. системы с похожими аттракторами. Теория хаоса обеспечивает прочный каркас для развития научных знаний.

Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех что можно себе представить. Системы динамических равенств использовались для моделирования всего - от роста популяций и эпидемий до аритмических сердцебиений.

В действительности, почти любая хаотическая система может быть смоделирована - рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов в отличие от точных соотношений; процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.

Фракталы находятся везде, наиболее заметны в графических программах как например очень успешная серия продуктов Fractal Design Painter. Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.

И, конечно, теория хаоса дает людям удивительно интересный способ того, как приобрести интерес к математике, одной из наиболее мало-популярной области познания на сегодняшний день.

БРОУНОВСКОЕ ДВИЖЕНИЕ И ЕГО ПРИМЕНЕНИЯ

Броуновское движение - это, например, случайное и хаотическое движение частичек пыли, взвешенных в воде. Этот тип движения, возможно, является аспектом фрактальной геометрии, имеющий с наибольшее практическое использование. Случайное Броуновское движение производит частотную диаграмму, которая может быть использована для предсказания вещей, включающих большие количества данных и статистики. Хорошим примером являются цены на шерсть, которые Мандельброт предсказал при помощи Броуновского движения.

Частотные диаграммы, созданные при построении графика на основе Броуновских чисел так же можно преобразовать в музыку. Конечно этот тип фрактальной музыки совсем не музыкален и может действительно утомить слушателя. Занося на график случайно Броуновские числа, можно получить Пылевой Фрактал наподобие того, что приведен здесь в качестве примера.

Кроме применения Броуновского движения для получения фракталов из фракталов, оно может использоваться и для создания ландшафтов. Во многих фантастических фильмах, как например Star Trek техника Броуновского движения была использована для создания инопланетных ландшафтов таких, как холмы и топологические картины высокогорных плато. Эти техники очень эффективны, и их можно найти в книге Мандельброта Фрактальная геометрия природы. Мандельброт использовал Броуновские линии для создания фрактальных линий побережья и карт островов (которые на самом деле были просто в случайном порядке изображенные точки) с высоты птичьего полета.

ДВИЖЕНИЕ БИЛЛИАРДНОГО ШАРИКА

Любой, кто когда либо брал в руки кий для бильярда, знает, что ключ к игре - точность. Малейшая ошибка в угле начального удара может быстро привести к огромной ошибке в положении шарика всего после нескольких столкновений. Эта чувствительность к начальным условиям называемая хаосом возникает непреодолимым барьером для любого, кто надеется предсказать или управлять траекторией движения шарика больше чем после шести или семи столкновений. И не стоит думать, что проблема заключается в пыли на столе или в нетвердой руке. Фактически, если вы используете ваш компьютер для построения модели, содержащей бильярдный стол, не обладающий ни каким трением, нечеловеческим контролем точности позиционирования кия, вам все равно не удастся предсказывать траекторию шарика достаточно долго!

Насколько долго? Это зависит частично от точности вашего компьютера, но в большей степени от формы стола. Для совершенно круглого стола, можно просчитать приблизительно до 500 положений столкновений с ошибкой около 0.1 процента. Но стоит изменить форму стола так, чтобы она стала хотя бы немножко неправильной (овальной), и непредсказуемость траектории может превышать 90 градусов уже после 10 столкновений! Единственный путь получить картинку общего поведения бильярдного шарика, отскакивающего от чистого стола - это изобразить угол отскока или длину дуги соответствующую каждому удару. Здесь приведены два последовательных увеличения такой фазово-пространственной картины.

Каждая отдельная петля или область разброса точек представляет поведение шарика, происходящее от одного набора начальных условий. Область картинки, на которой отображаются результаты какого-то одного конкретного эксперимента, называется аттракторной областью для данного набора начальных условий. Как можно видеть форма стола, использованного для этих экспериментов является основной частью аттракторных областей, которые повторяются последовательно в уменьшающемся масштабе. Теоретически, такое самоподобие должно продолжаться вечно и если мы будем увеличивать рисунок все больше и больше, мы бы получали все те же формы. Это называется очень популярным сегодня словом фрактал.

ИНТЕГРАЦИЯ ДЕТЕРМИНИРОВАННЫХ ФРАКТАЛОВ И ХАОС

Из рассмотренных примеров детерминистских фракталов можно увидеть, что они не проявляют никакого хаотического поведения и что они на самом деле очень даже предсказуемы. Как известно, теория хаоса использует фрактал для того, чтобы воссоздать или найти закономерности с целью предсказания поведения многих систем в природе, таких как, например, проблема миграции птиц.

Теперь давайте посмотрим, как это в действительности происходит. Используя фрактал, называемый Деревом Пифагора, не рассматриваемого здесь (который, кстати, не изобретен Пифагором и никак не связан с теоремой Пифагора) и Броуновского движения (которое хаотично), давайте попытаемся сделать имитацию реального дерева. Упорядочение листьев и веток на дереве довольно сложно и случайно и, вероятно не является чем-то достаточно простым, что может эмулировать короткая программа из 12 строк.

Для начала нужно сгенерировать Дерево Пифагора. Результат напоминает те старые детсадовские рисунки. Так что давайте сделаем ствол толще. На этой стадии Броуновское движение не используется. Вместо этого, каждый отрезок линии теперь стал линией симметрии прямоугольника, который становится стволом, и веток снаружи.

Но результат все еще выглядит слишком формальным и упорядоченным. Дерево еще не смотрится как живое. Попробуем применить некоторые из тех знаний в области детерминированных фракталов, которые мы только что приобрели.

Теперь можно использовать Броуновское движение для создания некоторой случайной беспорядочности, которая изменяет числа, округляя их до двух разрядов. В оригинале были использованы 39 разрядные десятичные числа. Результат (слева) не выглядит как дерево. Вместо этого, он выглядит как хитроумный рыболовный крючок!

Может быть округление до 2 разрядов было слишком много? Снова применяем Броуновское движение, округленное на этот раз до 7 разрядов. Результат по-прежнему выглядит как рыболовный крючок, но на этот раз в форме логарифмической спирали!

Так как левая сторона (содержащая все нечетные числа) не производит эффект крючка, случайные беспорядочности, произведенные Броуновским движением применяются дважды ко всем числам с левой стороны и только один раз к числам справа. Может быть этого будет достаточно чтобы исключить или уменьшить эффект логарифмической спирали. Итак, числа округляются до 24 разрядов. На этот раз, результат - приятно выглядящая компьютеризированная хаотическая эмуляция реального дерева.

РАЗДЕЛ 5: ДЕРЕВО ФЕЙГЕНБАУМА

ОБЩАЯ ИНФОРМАЦИЯ

Теория хаоса находит прямое применение в задаче моделирования роста популяций и рассматривается здесь на примере диаграммы Фейгенбаума, построенной с помощью программы LT Bifurcator.

БИФУРКАЦИИ В МОДЕЛЯХ ПОПУЛЯЦИЙ

Чудо фрактальной геометрии заключается в том, что чрезвычайно сложные формы могут получаться из таких простых процессов генерирования. Еще один сюрприз преподносит нам учение о динамических системах: такие простые, детерминированные уравнения могут порождать такое хаотическое поведение, при котором система никогда не возвращается в стабильное состояние и не проявляется никакой закономерности. Часто такие системы ведут себя вполне нормально до некоторого определенного значения ключевого параметра, потом испытывают переход и в котором существует две возможности дальнейшего развития, потом четыре, и, наконец, хаотический набор возможностей.

В 1786 году Томас Мальтус разработал математическую модель роста популяций и оказалось, что эта и другие модели подобного типа обладают описанным выше свойством. Предположим, что у нас есть модель в которой скорость роста популяции это функция, в частности, от численности популяции:

Новая популяция = скорость роста * старая популяция (1 – старая популяция)

Где популяция нормализована так, что она принимает значения от 0 до 1. Естественно, такая модель является сильно упрощенной и не может достаточно точно описывать динамику развития популяций. При скорости роста меньше 200%, эта модель стабильна, т.к. для любого начального значения, после нескольких поколений, численность популяции устанавливается на стабильном уровне. Но если скорость роста превышает 200%, кривая, графически отображающая уравнение, разделяется или бифурцирует на два дискретных решения, затем на четыре, и вскоре становится хаотической.

ДЕРЕВО ФЕЙГЕНБАУМА

Логистическое уравнение - это формула, над которой, в основном, работал Митчел Фейгенбаум при создании своей теории о фракталах. Эта формула должна описывать динамику развития популяции:

f(x) = (1 – x)rx

Простейшая модель - это пропорциональное соотношение численности с прошлым годом. Допустим в прошлом году у нас было x животных. В этом году их должно быть rx животных. Но это не выполняется в реальных условиях. Лучшее соответствие с реальностью получится если добавить фактор, зависящий от того какой потенциал существует у популяции для дальнейшего развития, и пусть x - коэффициент полноты, который меняется от 0 до 1. Потом добавляется фактор 1 – x, так что территория почти полностью заполнена, популяция не возрастет выше верхнего предела.

Расширяя логистическое выражение, получаем:

f(x) = аx – ах 2

Формула, использующаяся в программе LT Bifurcator для объяснения сущности фрактала Фейгенбаума - (1 + r)x – rx 2 не сильно отличается от формулы, приведенной выше. В принципе, для изучения теории можно было использовать любую формулу, например самую простую из формул данного вида - xІ – r. Единственными различиями являются различия в координатах окон на картинке и несколько измененный внешний вид изображения.

ПОЧЕМУ СИСТЕМА СТАНОВИТСЯ НЕПРЕДСКАЗУЕМОЙ?

Объяснение этому явлению дать не просто. Для каждой точки параметра r (по оси абсцисс), для функции x возможны следующие варианты. У функции могут быть:

· периодическая орбита, т.е. она периодически принимает одно или несколько значений, что происходит с фракталом, приведенным здесь в качестве иллюстрации на сегменте 0 < r < 2.57

· хаотическая орбита, т.е. она принимает такое большое количество различных значений при итерационном процессе, что невозможно найти какой-либо закономерности, как это можно было сделать в первом случае

· значения, не ограниченные по абсолютной величине, причем это происходит с обоих сторон дерева. Поэтому здесь уже невозможно отображать точки.

В первом случае, мы видим функцию, периодически принимающую определенные значения. При этом у дерева наблюдается одна или несколько ветвей. Число значений, которые принимает функция называется периодом итераций. У функции может быть период от одного до бесконечности.

Когда параметр пробегает значения от 0 до 2, период функции равен единице. В этом случае, соответствующее значение функции называется фиксированной точкой. Эта фиксированная точка оказывается решением уравнения

x = (1 + r)x – rx 2

1 + r)x – rx 2 – x = 0

Решения этого уравнения:

Отображая эти решения графически, мы видим, что один из графиков (для случая сложения членов в числителе) точно соответствует стеблю дерева Фейгенбаума вплоть до параметра, равного 2. Решения уравнения называются фиксированными точками. Так как только одно из решений совпадает с деревом Фейгенбаума и является результатом итераций, вторая функция дает притягивающие фиксированные точки.

x=(1+r)x - rx 2 ; r=2.1; x0=0.8

1.136	0.8199	1.1291	0.8234
0.8115	1.1299	0.8229	1.1287
1.1327	0.8215	1.1289	0.8235
0.817	1.1294	0.8232	1.1287
1.1309	0.8224	1.288	0.8236

При r = 2, фиксированная точка (т.е. одно из решений приведенного выше уравнения) перестает быть притягивающей фиксированной точкой и становится отталкивающей. С этого момента, функция уже никогда не сходится к одной точке. Далее начинается периодический цикл для функции, причем вначале функция колеблется между двумя точками. Анализируя полученные результаты, можно понять, что эти значения можно расценивать, как решения, полученные при итерации функции два раза. Давайте посмотрим, что будет, если мы запишем x как следующую функцию

x = [(1 + r)x – rx 2 ] 2 + (1+r)x

В результате получается четыре решения, причем первые два из них являются решениями исходного выражения. Это достаточно очевидно, что они тоже появляются здесь. Но интерес представляют третье и четвертое выражения. Если мы подставим в них 2.1 (значение, использовавшееся при составлении таблицы), то получим соответственно 1,128746121 и 0,823648487, т.е. те же значения, что и в таблице. Чего, собственно говоря, и следовало ожидать. Графическое изображение функции также представляет интерес. Фактически, мы получаем начало фегенбаумова дерева. Установленные факты можно использовать для расчета точек бифуркаций. Третье и четвертое уравнения не определены при значении параметра меньше 2, т.е. там, где линия разветвляется.

ОКНА В ДЕРЕВЕ ФЕЙГЕНБАУМА

Трудно сказать почему появляются окна в фейгенбаумовом дереве. Легче ответить на вопрос как они появляются. Это те области, для которых итерационным орбитам соответствуют нули. Например, если результат первой итерации дает в ответе 0, у нас появляется окно. Фактически это означает решение уравнения: 0 2 – r = 0

АТТРАКТОР И КОНСТАНТА ФЕЙГЕНБАУМА

АТТРАКТОР ФЕЙГЕНБАУМА

В отличие от константы Фейгенбаума, это число не является универсальным. Значение этого аттрактора зависит от того, какая используется формула. Для формулы, используемой в Lt Bifurcator x = (1 + r)x – rxІ графически можно найти значение приблизительно равное 2.56.

Число представляет значение параметра, при котором график первый раз проходит бесконечное количество бифуркаций. Это означает, что аттрактор Фейгенбаума - это хаотический аттрактор, т.к. функция никогда не проходит повторяющейся орбиты.

Чтобы просчитать это значение, можно использовать константу Фейгенбаума, но т.к. эта константа появляется только при многих буфуркациях если вам необходима приемлемая точность, практически это трудно реализуется и мне пока не удалось использовать этот метод.

Также следует заметить, что для всех окон на диаграмме Фейгенбаума, существует свое значение постоянной, при котором функция бифурцирует бесконечное количество раз.

КОНСТАНТА ФЕЙГЕНБАУМА

Если бы от меня требовался короткий ответ, я бы сказал: Это приблизительно 4.669211660910299067185320382047...

Однако это бы никого не удовлетворило. Вероятно это число является самым фантастическим фактом этого фрактала. Существует много формул, результатом которых является это дерево, но число все время остается одним и тем же. Стало уже почти легендой то обстоятельство, что Митчел Фейгенбаум позвонил домой маме, когда открыл универсальность и сказал, что это сделает его известным.

Знаменитая постоянная появляется, когда вы сравниваете длину одной части дерева, т.е. частей между линией бифуркаций (смотри иллюстрацию). Первая часть от 0 до 2. Ее длина равна 2. Следующая часть - от 2 до 2.448 и ее длина 0,448. Отношение между двумя длинами - 2/0.448 = 4,4642. В общем-то это достаточно близко к значению константы Фейгенбаума, но, согласно теории, результат можно улучшить, если взять предел отношения n+1 длины отрезка к n при n стремящемся к бесконечности (конечно это стремление ограничено аттрактором Фейгенбаума).

№ бифуркации	Точка бифуркации	Длина отрезка	Отношение длин

			4.4642
	2.448	0.448	4.7157
	2.543	0.095	4.5238
	2.564	0.021	4.5652
	2.5686	0.0046	4.1818
	2.5697	0.0011

Конечно, данный пример является просто примером и не претендует на какую-либо точность, т.к. данные получены достаточно быстро чисто графическим методом.

Важно запомнить, что с каждой бифуркацией требуется просчитать все больше и больше значений, чтобы получить точный результат, т.к. функции требуется больше итераций для стабилизации. Если вы пытаетесь построить дерево Фейгенбаума лишь по нескольким точкам, бифуркации последуют раньше, чем это есть на самом деле. Это становится все более важно при все большем и большем приближении дерева. Я использовал около 1000 итераций для значений, приведенных в таблице.

ГЕНЕРАЦИЯ СЛУЧАЙНЫХ ЧИСЕЛ

Посмотрите на распределение точек где-нибудь на правом краю дерева Фейгенбаума (Свойства -> Интервал -> Отрезок Псевдохаоса в программе Lt Bifurcator) Видите, они кажутся очень случайными. Так что кажется вполне оправданной идея использования этого для генерации случайных чисел.

Все что для этого может потребоваться - это запустить формулу x = (1 + r)x – rx 2 или какую-либо ей подобную и использовать последнее вычисленное значение каждый раз, когда требуется случайное число. Да это сработает: вы получите орбиту, которая никогда не повторяется, так как там хаос, но, к несчастью, я проверил распределение точек и результат не оказался равномерным, т.е. возможно, не равный для всех интервалов.

Числа, вычисленные по формуле всегда лежат между –2 и 2. Это легко растянуть на интервал от 0 до 9 и сделать числа целыми. Я сделал это и посчитал сколько попаданий получилось для каждого числа при проведении многих тысяч итераций. Вот результат:

r=1.99999, 50000 итераций

10276	3281	3668
4474	3157	4622
3640	3317	10193

среднее x: 4.501

стандартное отклонение x: 3.430

Нетрудно увидеть, что это не дает желаемого распределения. Но может быть взять значения, лежащие ближе к 3? Новый тест:

r=1.99999999999999, 50000 итераций

10162	3127	3722
4575	3202	4412
3800	3395	10204

среднее x: 4.489

стандартное отклонение x: 3.425

К сожалению, это дает нам почти такую же кривую распределения.

Примечание

Чтобы дать некоторое представление о среднем и стандартном отклонении: Если бы у нас был результат, который мы хотели получить, частота каждого числа между 0 и 9 была бы равна 5000, среднее значение было бы 4.5 и стандартное отклонение - 2.872.

ДЕРЕВО ФЕЙГЕНБАУМА И МНОЖЕСТВО МАНДЕЛЬБРОТА

Если вы когда-либо видели формулу множетсва Мандельброта z=z 2 + x, вы могли бы заметить схожесть между этой формулой и самой простой из формул для построения дерева Фейгенбаума x 2 – r. И это действительно так. Сходство существует. Но фейгенбаумово дерево растет в другую сторону. Измените формулу Фейгенбаума на x 2 + r и вы увидите сходство. Что касается множества Мандельброта, вам нужно смотреть вдоль горизонтальной оси, так как это единственная позиция в которой комплексная часть числа Мандельброта равна нулю. Вы увидите, что основное тело фигуры Мандельброта находится там, где функция в дереве Фейгенбаума принимает лишь одно значение. Когда происходит первое разделение линии (бифуркация) появляется новое тело на фигуре Мандельброта и т.д. Обратите также внимание на то, что когда в дереве открывается главное окно, на фигуре Мандельброта появляется дочернее тело.

Хаос - это порядок, который нужно расшифровать.

Жозе Сарамаго, «Двойник»

«Грядущим поколениям ХХ век будет памятен лишь благодаря созданию теорий относительности, квантовой механики и хаоса... теория относительности разделалась с иллюзиями Ньютона об абсолютном пространстве-времени, квантовая механика развеяла мечту о детерминизме физических событий, и, наконец, хаос развенчал Лапласову фантазию о полной предопределенности развития систем» . Эти слова известного американского историка и популяризатора науки Джеймса Глейка отражают огромную важность вопроса, который лишь вкратце освещается в статье, предлагаемой вниманию читателя. Наш мир возник из хаоса. Однако если бы хаос не подчинялся своим собственным законам, если бы в нем не было особой логики, он ничего не смог бы породить.

Новое - это хорошо забытое старое

Позволю себе еще одну цитату из Глейка:

Мысль о внутреннем подобии, о том, что великое может быть вложено в малое, издавна ласкает человеческую душу... По представлениям Лейбница, капля воды содержит в себе весь блистающий разноцветьем мир, где искрятся водяные брызги и живут другие неизведанные вселенные. «Увидеть мир в песчинке» - призывал Блейк, и некоторые ученые пытались следовать его завету. Первые исследователи семенной жидкости склонны были видеть в каждом сперматозоиде своего рода гомункулуса, т. е. крошечного, но уже полностью сформировавшегося человечка.

Ретроспективу подобных воззрений можно обратить гораздо дальше в глубь истории. Один из основных принципов магии - неотъемлемой ступени развития любого общества - состоит в постулате: часть подобна целому. Он проявлялся в таких действиях, как захоронение черепа животного вместо всего животного, модели колесницы вместо самой колесницы и т. д. Сохраняя череп предка, родственники считали, что он продолжает жить рядом с ними и принимать участие в их делах.

Еще древнегреческий философ Анаксагор рассматривал первичные элементы мироздания как частицы, подобные другим частицам целого и самому целому, «бесконечные и по множеству, и по малости». Аристотель характеризовал элементы Анаксагора прилагательным «подобочастные» .

А наш современник, американский кибернетик Рон Эглэш, исследуя культуру африканских племен и южноамериканских индейцев, сделал открытие: с древних времен некоторые из них использовали фрактальные принципы построения в орнаментах, узорах, наносимых на одежду и предметы быта, в украшениях, ритуальных обрядах и даже в архитектуре. Так, структура деревень некоторых африканских племен представляет собой круг, в котором находятся маленькие круги - дома, внутри которых еще более мелкие круги - дома духов. У иных племен вместо кругов элементами архитектуры служат другие фигуры, но они также повторяются в разных масштабах, подчиненных единой структуре. Причем эти принципы построения не были простым подражанием природе, но согласовывались с бытующим мировоззрением и социальной организацией .

Наша цивилизация, казалось бы, ушла далеко от первобытного существования. Однако мы продолжаем жить в том же мире, нас по-прежнему окружает природа, живущая по своим законам, несмотря на все попытки человека приспособить ее к своим нуждам. Да и сам человек (не будем забывать об этом) остается частью этой природы.

Герт Эйленбергер, немецкий физик, занявшийся изучением нелинейности, как-то заметил:

Почему силуэт согнувшегося под напором штормового ветра обнаженного дерева на фоне мрачного зимнего неба воспринимается как прекрасный, а очертания современного многофункционального здания, несмотря на все усилия архитектора, вовсе не кажутся такими? Сдается мне, что... наше чувство прекрасного «подпитывается» гармоничным сочетанием упорядоченности и беспорядка, которое можно наблюдать в естественных явлениях: облаках, деревьях, горных цепях или кристаллах снежинок. Все такие контуры суть динамические процессы, застывшие в физических формах, и для них типична комбинация устойчивости и хаотичности.

У истоков теории хаоса

Что мы понимаем под хаосом ? Невозможность предсказать поведение системы, беспорядочные скачки в разных направлениях, которые никогда не превратятся в упорядоченную последовательность.

Первым исследователем хаоса считается французский математик, физик и философ Анри Пуанкаре. Еще в конце XIX в. при изучении поведения системы с тремя телами, взаимодействующими гравитационно, он заметил, что могут быть непериодические орбиты, которые постоянно и не удаляются от конкретной точки, и не приближаются к ней.

Традиционные методы геометрии, широко используемые в естественных науках, основаны на аппроксимации структуры исследуемого объекта геометрическими фигурами, например линиями, плоскостями, сферами, метрическая и топологическая размерности которых равны между собой. В большинстве случаев свойства исследуемого объекта и его взаимодействие с окружающей средой описываются интегральными термодинамическими характеристиками, что приводит к утрате значительной части информации о системе и к замене ее на более или менее адекватную модель. Чаще всего подобное упрощение вполне оправдано, однако известны многочисленные ситуации, когда применение топологически неадекватных моделей недопустимо. Пример такого несоответствия привел в своей кандидатской диссертации (теперь уже доктор химических наук) Владимир Константинович Иванов: оно обнаруживается при измерении площади развитой (например, пористой) поверхности твердых тел с помощью сорбционных методов, регистрирующих изотермы адсорбции. Оказалось, что величина площади зависит от линейного размера молекул-«измерителей» не квадратично, чего следовало бы ожидать из простейших геометрических соображений, а с показателем степени, иногда вплотную приближающемся к трем .

Прогнозирование погоды - одна из проблем, над которой человечество бьется с древних времен. Существует известный анекдот на эту тему, где прогноз погоды передается по цепочке от шамана - оленеводу, затем геологу, потом редактору радиопередачи, и наконец круг замыкается, поскольку выясняется, что шаман узнал прогноз по радио. Описание такой сложной системы, как погода, со множеством переменных, невозможно свести к простым моделям. С данной задачи началось использование компьютеров для моделирования нелинейных динамических систем. Один из основоположников теории хаоса, американский метеоролог и математик Эдвард Нортон Лоренц много лет отдал проблеме прогнозирования погоды. Еще в 60-х годах прошлого века, пытаясь понять причины ненадежности прогнозов погоды, он показал, что состояние сложной динамической системы может сильно зависеть от начальных условий: незначительное изменение одного из многих параметров способно кардинально изменить ожидаемый результат. Лоренц назвал эту зависимость эффектом бабочки: «Сегодняшнее трепетание крыльев мотылька в Пекине через месяц может вызвать ураган в Нью-Йорке» . Ему принесла известность работа, посвященная общему круговороту атмосферы. Исследуя описывающую процесс систему уравнений с тремя переменными, Лоренц графически отобразил результаты своего анализа: линии графика представляют собой координаты точек, определяемых решениями в пространстве этих переменных (рис. 1). Полученная двойная спираль, названная аттрактор Лоренца (или «странный аттрактор»), выглядела как нечто бесконечно запутанное, но всегда расположенное в определенных границах и никогда не повторяющееся. Движение в аттракторе абстрактно (переменными могут быть скорость, плотность, температура и др.), и тем не менее оно передает особенности реальных физических явлений, таких как движение водяного колеса, конвекция в замкнутой петле, излучение одномодового лазера, диссипативные гармонические колебания (параметры которых играют роль соответствующих переменных).

Из тысяч публикаций, составивших специальную литературу по проблеме хаоса, вряд ли какая-либо цитировалась чаще, чем написанная Лоренцем в 1963 г. статья «Детерминистский непериодический поток» . Хотя благодаря компьютерному моделированию уже во времена этой работы предсказание погоды из «искусства превратилось в науку», долгосрочные прогнозы по-прежнему оставались недостоверными и ненадежными. Причина этого заключалась в том самом эффекте бабочки.

В тех же 60-х годах математик Стивен Смэйл из Калифорнийского университета собрал в Беркли исследовательскую группу из молодых единомышленников. Ранее он был удостоен медали Филдса за выдающиеся исследования в области топологии. Смэйл занимался изучением динамических систем, в частности нелинейных хаотических осцилляторов. Для воспроизведения всей неупорядоченности осциллятора ван дер Поля в фазовом пространстве он создал структуру, известную под названием «подкова» - пример динамической системы, имеющей хаотическую динамику.

«Подкова» (рис. 2) - точный и зримый образ сильной зависимости от начальных условий: никогда не угадаешь, где окажется начальная точка после нескольких итераций. Этот пример послужил толчком к изобретению русским математиком, специалистом по теории динамических систем и дифференциальных уравнений, дифференциальной геометрии и топологии Дмитрием Викторовичем Аносовым «диффеоморфизмов Аносова» . Позже из этих двух работ выросла теория гиперболических динамических систем. Прошло десятилетие, прежде чем результаты работы Смэйла удостоились внимания представителей других дисциплин. «Когда это все же случилось, физики поняли, что Смэйл повернул целый раздел математики лицом к реальному миру» .

В 1972 г. математик из Мэрилендского университета Джеймс Йорк прочитал вышеупомянутую статью Лоренца, которая поразила его. Йорк увидел в статье живую физическую модель и посчитал своей святой обязанностью донести до физиков то, чего они не разглядели в работах Лоренца и Смэйла. Он направил копию статьи Лоренца Смэйлу. Тот изумился, обнаружив, что безвестный метеоролог (Лоренц) десятью годами раньше обнаружил ту неупорядоченность, которую он сам посчитал однажды математически невероятной, и разослал копии всем своим коллегам.

Биолог Роберт Мэй, друг Йорка, занимался изучением изменений численности популяций животных. Мэй шел по стопам Пьера Ферхлюста, который еще в 1845 г. обратил внимание на непредсказуемость изменения численности животных и пришел к выводу, что коэффициент прироста популяции - величина непостоянная. Иными словами, процесс оказывается нелинейным. Мэй пытался уловить, что случается с популяцией в момент приближения колебаний коэффициента роста к некоторой критической точке (точке бифуркации). Варьируя значения этого нелинейного параметра, он обнаружил, что возможны коренные перемены в самой сущности системы: увеличение параметра означало возрастание степени нелинейности, что, в свою очередь, изменяло не только количественные, но и качественные характеристики результата. Подобная операция влияла как на конечное значение численности популяции, находившейся в равновесии, так и на ее способность вообще достигнуть последнего. При определенных условиях периодичность уступала место хаосу, колебаниям, которые никогда не затухали.

Йорк математически проанализировал описанные явления в своей работе, доказав, что в любой одномерной системе происходит следующее: если появляется регулярный цикл с тремя волнами (плавными подъемами и спадами значений какого-либо параметра), то в дальнейшем система начнет демонстрировать как правильные циклы любой другой продолжительности, так и полностью хаотичные. (Как выяснилось через несколько лет после опубликования статьи на международной конференции в восточном Берлине, советский (украинский) математик Александр Николаевич Шарковский несколько опередил Йорка в своих исследованиях ). Йорк написал статью для известного научного издания «Американский математический ежемесячник» . Однако Йорк достиг большего, чем просто математический результат: он продемонстрировал физикам, что хаос вездесущ, стабилен и структурирован. Он дал повод поверить в то, что сложные системы, традиционно описывающиеся трудными для решения дифференциальными уравнениями, могут быть представлены с помощью наглядных графиков.

Мэй пытался привлечь внимание биологов к тому, что популяции животных переживают не одни лишь упорядоченные циклы. На пути к хаосу возникает целый каскад удвоения периодов. Именно в точках бифуркации некоторое увеличение плодовитости особей могло привести, например, к смене четырехгодичного цикла популяции непарного шелкопряда восьмигодичным. Американец Митчел Фейгенбаум решил начать с подсчета точных значений параметра, порождавших такие изменения. Его расчеты показывали, что не имело значения, какова начальная популяция, - она все равно неуклонно приближалась к аттрактору. Затем, с первым удвоением периодов, аттрактор, подобно делящейся клетке, раздваивался. Потом происходило следующее умножение периодов, и каждая точка аттрактора вновь начинала делиться. Число - инвариант, полученный Фейгенбаумом, - позволило ему предугадывать, когда именно это произойдет. Ученый обнаружил, что может прогнозировать этот эффект для сложнейшего аттрактора - в двух, четырех, восьми точках... Говоря языком экологии, он мог прогнозировать действительную численность, которая достигается в популяциях во время ежегодных колебаний. Так Фейгенбаум открыл в 1976 г. «каскад удвоения периода», опираясь на работу Мэя и свои исследования турбулентности. Его теория отражала естественный закон, который относится ко всем системам, испытывающим переход от упорядоченного состояния к хаосу. Йорк, Мэй и Файгенбаум первыми на Западе в полной мере осознали важность удвоения периодов и сумели передать эту идею всему научному сообществу. Мэй заявлял, что хаос необходимо преподавать.

Советские математики и физики продвигались в своих исследованиях независимо от зарубежных коллег. Начало изучению хаоса положили работы А. Н. Колмогорова 50-х годов. Но и идеи зарубежных коллег не оставались без их внимания. Пионерами теории хаоса считаются советские математики Андрей Николаевич Колмогоров и Владимир Игоревич Арнольд и немецкий математик Юрген Мозер, построившие теорию хаоса, называемую КАМ (теория Колмогорова - Арнольда - Мозера). Другой наш выдающийся соотечественник, блестящий физик и математик Яков Григорьевич Синай, применил в термодинамике соображения, аналогичные «подкове Смейла». Едва в 70-х годах с работой Лоренца познакомились западные физики, как она приобрела известность и в СССР. В 1975 г., когда Йорк и Мэй еще прилагали немалые усилия к тому, чтобы добиться внимания коллег, Синай и его товарищи организовали в Горьком исследовательскую группу для изучения этой проблемы.

В прошлом веке, когда узкая специализация и разобщение между различными дисциплинами стали в науке нормой, математики, физики, биологи, химики, физиологи, экономисты бились над схожими задачами, не слыша друг друга. Идеи, требующие изменения привычного мировоззрения, всегда с трудом пробивают себе путь. Однако постепенно стало ясно, что такие вещи, как изменение популяций животных, колебания цен на рынке, перемена погоды, распределение небесных тел по размерам и многое, многое другое, - подчиняются одним закономерностям. «Осознание этого факта заставило менеджеров пересмотреть отношение к страховке, астрономов - под другим углом зрения взглянуть на Солнечную систему, политиков - изменить мнение о причинах вооруженных конфликтов» .

К середине 80-х годов ситуация сильно изменилась. Идеи фрактальной геометрии объединили ученых, озадаченных собственными наблюдениями и не знавшими, как их интерпретировать. Для исследователей хаоса математика стала экспериментальной наукой, компьютеры заменили собой лаборатории. Графические изображения приобрели первостепенную важность. Новая наука дала миру особый язык, новые понятия: фазовый портрет, аттрактор, бифуркация, сечение фазового пространства, фрактал...

Бенуа Мандельброт, опираясь на идеи и работы предшественников и современников, показал, что такими сложными процессами, как рост дерева, образование облаков, вариации экономических характеристик или численности популяций животных управляют сходные, по сути, законы природы. Это определенные закономерности, по которым живет хаос. С точки зрения природной самоорганизации они намного проще, чем искусственные формы, привычные цивилизованному человеку. Сложными их можно признать лишь в контексте евклидовой геометрии, поскольку фракталы определяются посредством задания алгоритма, и, следовательно, могут быть описаны с помощью небольшого объема информации.

Фрактальная геометрия природы

Давайте попробуем разобраться, что же такое фрактал и «с чем его едят». А съесть некоторые из них действительно можно, как, например, типичного представителя, показанного на фотографии.

Слово фрактал происходит от латинского fractus - дробленый, сломанный, разбитый на куски. Под фракталом подразумевается математическое множество, обладающее свойством самоподобия, т. е. масштабной инвариантности.

Термин «фрактал» был придуман Мандельбротом в 1975 г. и получил широкую популярность с выходом в 1977 г. его книги «Фрактальная геометрия природы» . «Дайте чудовищу какое-нибудь уютное, домашнее имя, и вы удивитесь, насколько легче будет его приручить!» - говорил Мандельброт. Это стремление сделать исследуемые объекты (математические множества) близкими и понятными привело к рождению новых математических терминов, таких как пыль , творог , сыворотка , наглядно демонстрирующих их глубинную связь с природными процессами.

Математическое понятие фрактала выделяет объекты, обладающие структурами различных масштабов, как больших, так и малых, и, таким образом, отражает иерархический принцип организации. Конечно, различные ветви дерева, например, не могут быть точно совмещены друг с другом, но их можно считать подобными в статистическом смысле. Точно так же формы облаков, очертания гор, линия морского берега, рисунок пламени, сосудистая система, овраги, молния, рассматриваемые при различных масштабах, выглядят подобными. Хотя эта идеализация и может оказаться упрощением действительности, она существенно увеличивает глубину математического описания природы.

Понятие «природный фрактал» Мандельброт ввел для обозначения естественных структур, которые могут быть описаны с помощью фрактальных множеств. Эти природные объекты включают в себя элемент случайности. Созданная Мандельбротом теория позволяет количественно и качественно описывать все те формы, которые ранее назывались спутанными, волнистыми, шероховатыми и т. д.

Динамические процессы, о которых шла речь выше, так называемые процессы с обратной связью, возникают в различных физических и математических задачах. Все они имеют одно общее - конкуренцию нескольких центров (получивших имя «аттракторы») за доминирование на плоскости. То состояние, в котором система оказалась после некоторого числа итераций, зависит от ее «места старта». Поэтому каждому аттрактору соответствует некоторая область начальных состояний, из которых система обязательно попадет в рассматриваемое конечное состояние. Таким образом, фазовое пространство системы (абстрактное пространство параметров, ассоциированных с конкретной динамической системой, точки в котором однозначно характеризуют все возможные ее состояния) разбивается на области притяжения аттракторов. Налицо своеобразный возврат к динамике Аристотеля, согласно которой каждое тело стремится к предназначенному ему месту . Простые границы между «сопредельными территориями» в результате такого соперничества возникают редко. Именно в этой пограничной области и происходит переход от одной формы существования к другой: от порядка к хаосу. Общий вид выражения для динамического закона очень прост: х n+1 → f х n C . Вся сложность состоит в нелинейной зависимости между начальным значением и результатом. Если начать итерационный процесс указанного вида с некоторого произвольного значения \(x_0 \), то результатом его будет последовательность \(x_1 \), \(x_2 \), ..., которая либо будет сходиться к некоторому предельному значению \(X \), стремясь к состоянию покоя, либо придет к некоторому циклу значений, которые будут повторяться вновь и вновь, либо будет все время вести себя беспорядочно и непредсказуемо . Именно такие процессы исследовали еще во время Первой мировой войны французские математики Гастон Жюлиа и Пьер Фато.

Изучая множества, открытые ими, Мандельброт в 1979 г. пришел к изображению на комплексной плоскости образа, который является, как будет ясно из дальнейшего, своего рода оглавлением целого класса форм, именующегося множествами Жюлиа. Множество Жюлиа - это множество точек, возникающее в результате итерирования квадратичного преобразования: х n → х n−1 2 + C , динамика в окрестности которых неустойчива по отношению к малым возмущениям начального положения. Каждое последовательное значение \(x \) получается из предыдущего; комплексное число \(C \) называется управляющим параметром . Поведение последовательности чисел зависит от параметра \(C \) и начальной точки \(x_0 \). Если зафиксировать \(C \) и изменять \(x_0 \) в поле комплексных чисел, мы получим множество Жюлиа. Если же зафиксировать \(x_0 \) = 0 и изменять \(C \), получим множество Мандельброта (\(M \)). Оно подсказывает нам, какого вида множества Жюлиа следует ожидать при конкретном выборе \(C \). Каждое комплексное число \(C \) либо принадлежит области \(M \) (черной на рис. 3), либо нет. \(C \) принадлежит \(M \) тогда и только тогда, когда «критическая точка» \(x_0 \) = 0 не стремится к бесконечности. Множество \(M \) состоит из всех точек \(C \), которые ассоциируются со связными множествами Жюлиа, если же точка \(C \) лежит вне множества \(M \), ассоциированное с ней множество Жюлиа несвязно. Граница множества \(M \) определяет момент математического фазового перехода для множеств Жюлиа х n → х n−1 2 + C . Когда параметр \(C \) покидает \(M \), множества Жюлиа теряют свою связность, образно говоря, взрываются и превращаются в пыль. Качественный скачок, происходящий на границе \(M \), влияет и на примыкающую к границе область. Сложную динамическую структуру пограничной области можно приближенно показать, окрашивая (условно) в разные цвета зоны с одинаковым временем «убегания в бесконечность начальной точки \(x_0 \) = 0». Те значения \(C \) (один оттенок), при которых критической точке требуется данное число итераций, чтобы оказаться вне круга радиусом \(N \), заполняют промежуток между двумя линиями. По мере приближения к границе \(M \) необходимое число итераций увеличивается. Точка все большее время вынуждена блуждать извилистыми путями вблизи множества Жюлиа. Множество Мандельброта воплощает в себе процесс перехода от порядка к хаосу.

Интересно проследить путь, которым Мандельброт шел к своим открытиям. Бенуа родился в Варшаве в 1924 г., в 1936 семья эмигрировала в Париж. Окончив Политехническую школу, а затем и университет в Париже, Мандельброт переехал в США, где отучился еще и в Калифорнийском технологическом институте. В 1958 г. он устроился в научно-исследовательский центр IBM в Йорктауне. Несмотря на чисто прикладную деятельность компании, занимаемая должность позволяла ему вести исследования в самых разных областях. Работая в области экономики, молодой специалист занялся изучением статистики цен на хлопок за большой период времени (более 100 лет). Анализируя симметрию длительных и кратковременных колебаний цен, он заметил, что эти колебания в течение дня казались случайными и непредсказуемыми, однако последовательность таких изменений не зависела от масштаба. Для решения этой задачи он впервые использовал свои разработки будущей фрактальной теории и графическое отображение исследуемых процессов.

Интересуясь самыми разными областями науки, Мандельброт обратился к математической лингвистике, затем наступил черед теории игр. Он также предложил собственный подход к экономике, указав на упорядоченность масштабов в распространении малых и больших городов. Изучая малоизвестную работу английского ученого Льюиса Ричардсона, вышедшую после смерти автора, Мандельброт столкнулся с феноменом береговой линии. В статье «Какова длина береговой линии Великобритании?» он подробно исследует этот вопрос, над которым мало кто задумывался до него, и приходит к неожиданным выводам: длина береговой линии равна... бесконечности! Чем точнее вы стараетесь ее измерить, тем большим получается ее значение!

Для описания подобных явлений Мандельброту пришло в голову отталкиваться от идеи размерности. Фрактальная размерность объекта служит количественной характеристикой одной из его особенностей, а именно - заполнения им пространства.

Определение понятия фрактальной размерности восходит к работе Феликса Хаусдорфа, опубликованной в 1919 г., и было окончательно сформулировано Абрамом Самойловичем Безиковичем. Фрактальная размерность - мера детализации, изломанности, неровности фрактального объекта. В евклидовом пространстве топологическая размерность всегда определяется целым числом (размерность точки - 0, линии - 1, плоскости - 2, объемного тела - 3). Если проследить, например, проекцию на плоскость движения броуновской частицы, которая вроде бы должна состоять из отрезков прямой, т. е. иметь размерность 1, очень скоро окажется, что след ее заполняет почти всю плоскость. Но размерность плоскости - 2. Расхождение между этими величинами и дает нам право отнести данную «кривую» к фракталам, а ее промежуточную (дробную) размерность называть фрактальной. Если рассмотреть хаотическое движение частицы в объеме, фрактальная размерность траектории окажется больше 2, но меньше 3. Артерии человека, например, имеют фрактальную размерность примерно 2,7. Упомянутые в начале статьи результаты Иванова, относящиеся к измерению площади пор силикагеля, которые не могут быть истолкованы в рамках обычных евклидовых представлений, при использовании теории фракталов находят разумное объяснение .

Итак, с математической точки зрения, фракталом называется множество, для которого размерность Хаусдорфа - Безиковича строго больше его топологической размерности и может быть (а чаще всего и является) дробной.

Необходимо особо подчеркнуть, что фрактальная размерность объекта не описывает его форму, и объекты, имеющие одинаковую размерность, но порожденные различными механизмами образования, зачастую совершенно не похожи друг на друга. Физические фракталы обладают скорее статистическим самоподобием.

Дробное измерение позволяет вычислять характеристики, которые не могут быть четко определены иным путем: степени неровности, прерывистости, шероховатости или неустойчивости какого-либо объекта. Например, извилистая береговая линия, несмотря на неизмеримость ее длины, обладает присущей только ей шероховатостью. Мандельброт указал пути расчета дробных измерений объектов окружающей действительности. Создавая свою геометрию, он выдвинул закон о неупорядоченных формах, которые встречаются в природе. Закон гласил: степень нестабильности постоянна при различных масштабах.

Особую разновидность фракталов составляют временные фракталы . В 1962 г. Мандельброт столкнулся с задачей по устранению шумов в телефонных линиях, которые вызвали проблемы для компьютерных модемов. Качество передачи сигнала зависит от вероятности возникновения ошибок. Инженеры бились над проблемой уменьшения шумов, придумывая головоломные и дорогостоящие приемы, но не получали впечатляющих результатов. Опираясь на работу основателя теории множеств Георга Кантора, Мандельброт показал, что возникновения шумов - порождения хаоса - невозможно избежать в принципе, поэтому предложенные способы борьбы с ними не принесут результата. В поисках закономерности возникновения шумов он получает «канторову пыль» - фрактальную последовательность событий. Интересно, что тем же закономерностям подчиняется распределение звезд в Галактике:

«Вещество», однородно распределенное вдоль инициатора (единичный отрезок временной оси), подвергается воздействию центробежного вихря, который «сметает» его к крайним третям интервала... Створаживанием можно называть любой каскад неустойчивых состояний, приводящий в итоге к сгущению вещества, а термин творог может определять объем, внутри которого некая физическая характеристика становится - в результате створаживания - чрезвычайно концентрированной.

Хаотические явления, такие как турбулентность атмосферы, подвижность земной коры и т. д., демонстрируют сходное поведение в различных временных масштабах подобно тому, как объекты, обладающие инвариантностью к масштабу, обнаруживают сходные структурные закономерности в различных пространственных масштабах.

В качестве примера приведем несколько характерных ситуаций, где полезно использовать представления о фрактальной структуре. Профессор Колумбийского университета Кристофер Шольц специализировался на изучении формы и строения твердого вещества Земли, он изучал землетрясения. В 1978 г. он прочитал книгу Мандельброта «Фракталы: форма, случайность и размерность» и попытался применить теорию к описанию, классификации и измерению геофизических объектов. Шольц выяснил, что фрактальная геометрия снабдила науку эффективным методом описания специфичного бугристого ландшафта Земли. Фрактальное измерение ландшафтов планеты открывает двери к постижению ее важнейших характеристик. Металлурги обнаружили то же самое на другом масштабном уровне - применительно к поверхностям различных типов стали. В частности, фрактальное измерение поверхности металла зачастую позволяет судить о его прочности. Огромное количество фрактальных объектов продуцирует явление кристаллизации. Самый распространенный тип фракталов, возникающих при росте кристаллов, - дендриты, они чрезвычайно широко распространены в живой природе. Ансамбли наночастиц часто демонстрируют реализацию «пыли Леви». Эти ансамбли в сочетании с абсорбированным растворителем образуют прозрачные компакты - стекла Леви, потенциально важные материалы фотоники .

Поскольку фракталы выражаются не в первичных геометрических формах, а в алгоритмах, наборах математических процедур, понятно, что такая область математики стала развиваться семимильными шагами вместе с появлением и развитием мощных компьютеров. Хаос, в свою очередь, вызвал к жизни новые компьютерные технологии, специальную графическую технику, которая способна воспроизводить удивительные структуры невероятной сложности, порождаемые теми или иными видами беспорядка. В век Интернета и персональных компьютеров то, что представляло значительную сложность во времена Мандельброта, стало легко доступным любому желающему. Но самым важным в его теории стало, разумеется, не создание красивых картинок, а вывод, что данный математический аппарат пригоден для описания сложных природных явлений и процессов, которые раньше не рассматривались в науке вообще. Репертуар алгоритмических элементов неисчерпаем.

Овладев языком фракталов, можно описать форму облака так же четко и просто, как архитектор описывает здание с помощью чертежей, в которых применяется язык традиционной геометрии. <...> Прошло всего несколько десятилетий с тех пор, как Бенуа Мандельброт заявил: «Геометрия природы фрактальна!», на сегодняшний день мы уже можем предположить намного больше, а именно что фрактальность - это первоочередной принцип построения всех без исключения природных объектов.

В заключение позвольте представить вашему вниманию набор фотографий, иллюстрирующих этот вывод, и фракталов, построенных с помощью компьютерной программы Fractal Explorer . А проблеме использования фракталов в физике кристаллов будет посвящена наша следующая статья.

Post Scriptum

С 1994 по 2013 г. в пяти томах вышел уникальный труд отечественных ученых «Атлас временных вариаций природных антропогенных и социальных процессов» - не имеющий аналогов источник материалов, который включает в себя данные мониторинга космоса, биосферы, литосферы, атмосферы, гидросферы, социальной и техногенной сфер и сферы, связанной со здоровьем и качеством жизни человека. В тексте подробно приводятся данные и результаты их обработки, сопоставляются особенности динамики временных рядов и их фрагментов. Унифицированное представление результатов дает возможность получить сопоставимые результаты для выявления общих и индивидуальных черт динамики процессов и причинно-следственных связей между ними. На экспериментальном материале показано, что процессы в разных сферах, во-первых, схожи, а во-вторых, в большей или меньшей степени связаны друг с другом.

Итак, атлас обобщил результаты междисциплинарных исследований и представил сравнительный анализ совершенно различных данных в широчайшем диапазоне времени и пространства. Книга показывает, что «протекающие в земных сферах процессы обусловлены большим числом взаимодействующих факторов, которые в разных областях (и в разное время) вызывают разную реакцию», что говорит о «необходимости комплексного подхода к анализу геодинамических, космических, социальных, экономических и медицинских наблюдений». Остается выразить надежду на то, что эти фундаментальные по значимости работы будут продолжены.

. Юргенс Х., Пайтген Х.-О., Заупе Д. Язык фракталов // В мире науки. 1990. № 10. С. 36–44.
. Атлас временных вариаций природных антропогенных и социальных процессов. Т. 1: Порядок и хаос в литосфере и других сферах. М., 1994; Т. 2: Циклическая динамика в природе и обществе. М., 1998; Т. 3: Природные и социальные сферы как части окружающей среды и как объекты воздействий. М., 2002; Т. 4: Человек и три окружающие его среды. М., 2009. Т. 5: Человек и три окружающие его среды. М., 2013.

ЗОЛОТАЯ ПРОПОРЦИЯ, ФРАКТАЛЫ И ХАОС

В СВЯЗИ С НЕКОТОРЫМИ ПРЕДСТАВЛЕНИЯМИ О МИРОЗДАНИИ

Сокольчук К.Ю., Остапович В.В. (Научно-технический центр «Булат НВР», г.Киев, Украина)

Определение. Фракталом будем называть структуру, состоящую из частей, которые в каком-то смысле подобны целому. Сам термин "фрактал" означает "дробный". Когда вы всматриваетесь во фрактальную форму, то видите одну и ту же структуру независимо от степени увеличения. Такое подобие можно увидеть в природе, рассматривая при разном приближении горы, облака, береговые линии и т.п. Его можно встретить, исследуя формы молекул или галактик. Фрактальность стремительно становится одной из самых емких метафор для объяснения и понимания мира.

Однако абсолютно точного определения фрактала не существует. Возможно, когда-нибудь оно будет найдено, но такого может и не случиться ввиду того, что фрактальная геометрия есть геометрия природы. Дефиниция фрактала стоит в одном ряду с дефиницией природы.

Концепция фрактальности мироздания и отдельных его элементов возникла во второйполовине ХХ века в рамках новой научной парадигмы, объединяющей синергетику, кибернетику, информатику и другие теории, имеющие универсальное значение для любых явлений бытия. Фрактальная гипотеза базируется на представлениях теории хаоса и нелинейных динамических систем. В силу этого, а также некоторых других свойств (иерархичность структуры, обратная связь, чувствительность к начальным условиям и т.п.), фрактальные объекты обладают повышенной устойчивостью и приспособляемостью к внешним условиям по сравнению со статическими системами.

Математический алгоритм построения фракталов мироздания. Для математическогомоделирования построения фракталов, как нелинейных динамических систем, общепринято использовать рекуррентные формулы. Объекты, построенные с помощью рекурсии, обладают внутренним самоподобием и устойчивостью к ошибкам (случайным и систематическим). Кроме того, и это представляется важным, рекурсия – необходимое свойство автокреационных (т.е. строящих сами себя) систем. Нами в качестве алгоритма был выбран суммационный ряд Фибоначчи, т.к. в различных объектах природы (прежде всего, «живой») он проявляется слишком часто, что бы это было случайностью.

Результаты моделирования фрактальных объектов Фибоначчи.

Следуя работам проф. А.П.Стахова, обобщим формулу Бине (генерирующую ряд Фибоначчи) на множество всех действительных чисел. Полученную функцию:

F(x) =(φ x -(-φ) -x)/√5 ( 1)

будем называть «программа Фибоначчи». Как и для ряда Фибоначчи, для нее на множестве действительных чисел выполняются соотношения:

F(x+1) = F(x) + F(x-1) (2)

F(x+1)/F(x) → φпри х→ +∞,φ = (1+√5)/2 = 1,6180… (3)

F(x+1)/F(x) → -1/φ при х→ - ∞ (4)

Функция F(x) принадлежитобласти комплексных чисел, только в отдельных точках выходя в область действительных(при х целочисленном). Фазовый портрет программы Фибоначчи (в общем случае) – спираль и затухающая синусоида (рис.1) вдоль оси Х(действительной части комплексного числа).

а)б)

Рис.1. Фазовый портрет обобщенного ряда Фибоначчи на плоскости комплексных чисел (а)и положение спирали программы Фибоначчи в пространстве (б).

Уравнение (2) , как функцию от начальных условий х 0 , х 1 и количества циклов х , представим в виде:

F(x+1, x 0 , x 1) = x 1 *F(x) + x 0 *F(x-1) (5)

Уравнение (5)описывает множество неких дискретных объектов, построенных по программе Фибоначчи, структура которых подобна, а отличие заключается лишь в масштабных (выбор начальных условий х 0 и х 1) и (или) временных (х – количество циклов) параметрах. Т.о., мы имеем дело с программой (обобщение формулы Бине), обеспечивающей рекуррентные соотношения в области комплексных чисел. Следуя представлениям, развитым Б.Мандельбротом, это необходимо и достаточно для образования фрактальных объектов в определенной области (х, х 0 , х 1). Учтем, что подобие иерархических структур, выражаемое через золотое сечение φ , приближается к идеальному с ростом х (количества циклов), и выбор максимально отличных друг от друга начальных условий (на порядки) лишь несущественно увеличивает количество циклов для достижения требуемой точности оценки φ . Тогда весь пространственно-временной континуум можно представить как единый фрактальный объект, отдельные элементы которого являются аттракторами фракталов следующего, более низкого иерархического уровня.

Рассмотрим вопрос внутреннего подобия этой структуры более подробно. Развертка по времени (т.е. х 0 и х 1 – const) обеспечивает подобие соседних иерархических уровней, выражаемое как φ (что очевидно, в соответствии с формулой (3)). Не требует доказательства и то, что для уровней х и х-2 подобие выражается как φ 2 . В общем случае для уровней х и х-n, их отношение равно φ n . В области отрицательных значений циклов х подобие в общем случае имеет вид: 1/(-φ) n . Развертку в пространстве рассмотрим на примере х и х 1 – const, а переменной будет х 0 . При х 0 = 0 или 2 и х 1 = 1 имеем, соответственно, тривиальные ряды Фибоначчи и Люка. Их отношение (что следует просто из формулы Бине) при одинаковом количестве циклов х равно √5 или, что тоже самое: φ + 1/φ. В случае х 0 = 3 (т.е. ряд, следующий после Люка) отношение выражается как φ 2 + 1/φ 3 =2,854… Дальше картина принципиально не изменяется. Подобие при пространственной развертке может быть записано с помощью только двух чисел – 1 и φ, а также элементарных математических операций с ними (+, -, *, :). Вероятно, можно вывести и общую формулу. Таким образом, если «наш мир» построен по программе Фибоначчи, мы должны во всех многочисленных его проявлениях находить каким-то образом «золотое сечение» - φ. В действительности это наблюдается, главным образом, у материальных объектов, которые принято называть «живой» материей. Причина заключается, на наш взгляд, в том, что в большинстве случаев мы рассматриваем развертку объекта в сечении, где переменными являются все три параметра – х, х 0 , х 1 . Например, периодическая система элементов Менделеева. Все элементы образовывались на различных циклах (этапах) развития Вселенной и при различных начальных условиях (условно говоря – температура, масса, энтропия и др. характеристики аттракторов). Искать в их структуре какое-то регулярное подобие, выражаемое численно через φ и 1, дело бессмысленное. Аналогично, массы планет или их радиусы, или радиусы орбит вращения не удается описать через «золотую гармонию», несмотря на многочисленные попытки. С другой стороны, объекты «живой» материи, и человек в том числе, как целостные объекты с фиксированными начальными условиями и возможностью наблюдения их на всех циклах развития несут в морфологическом строении и функционировании гармонию, выражаемую через φ. (Фактические данные мы не приводим, они есть на сайте «Музей золотой гармонии», созданном проф. А.П.Стаховым).

Т.о., структура и топология нашей Вселенной может быть закодирована с помощью только двух чисел – 1 и φ в рамках описания развития, как выполнения программы Фибоначчи. Очевидно, эти числа первичны, поскольку с их помощдвухью записана и выполняется программа. Как появились они, в то время когда Творец еще только «писал» программу построения Вселенной?Представим себе, что программа в виде символов написана, структурирована или упакована (термины могут быть любыми) как автокреационный объект, у которого каждый последующий уровень есть функция двух предыдущих(программа Фибоначчи). Выберем три соседних иерархических уровня. Значение φ просто следует из отношения ближайших уровней. Отношение трех соседних уровней фактически сводится к известному соотношению:φ 2 = φ + 1 или φ 2 – φ = 1. Таким образом, сама запись программы генерирует два первочисла φ и 1. Как показано проф. Стаховым А.П., системы счисления и кодирования информации с использованием φ имеютпреимущества перед другими (десятичная, двоичная и пр.) в части нахождения ошибок, их дифференциации и исправления. Для корректного выполнения программы развития эти свойства представляются исключительно важными.

Взаимодействие объектов программы Фибоначчи и их графика.

Принимая концепцию (или гипотезу) глобального взаимодействия объектов Мироздания, на настоящем этапе исследования в качестве механизмов взаимодействия фракталов мы применяли элементарные алгебраические операции сложения, умножения и т.д. Для отображения получаемых структур использовалась компьютерная 3-D графика. Следует учитывать, что возникающие при взаимодействии фракталов структуры в общем случае n-мерны, поэтому получаемые изображения по сути являются трехмерными сечениями в «плоскости» циклов развития отдельных составляющих.

А) Счетчики циклов развития взаимодействующих объектов совпадают.

Рис.2аРис.2б

Рис.2 Фазовый портрет (2а) и вид в трехмерном пространстве (2б) объекта, полученного из отношения объектов Фибоначчи и Люка (начальные условия 0 и 1 ; 2 и 1, соответственно).Обозначения на рис.2б – оси Х и У – действительная и мнимая часть объекта, ось Z – счетчик циклов (один для Фибоначчи и Люка).

Фазовый портрет объекта (рис.2а) в целом очень похож на известное символьное изображение принципа Мироздания:

Очевидно, неслучайно, в некоторых работах ряды Фибоначчи и Люка рассматривают как мужское и женское начало (Инь и Ян). Не последнее место узор рисунка 2а занимает и в философско-художественных представлениях людей, проживавших на нашей земле.

Б) В случае, когда счетчики циклов взаимодействующих объектов не совпадают, вместо параметрических кривых (рис.1б и 2б) мы получаем трехмерные поверхности как сечения «плоскостью» циклов (времени).

Рис.3. Сложение фракталов Фибоначчи и Люка. Координатные оси в горизонтальной плоскости – действительная и мнимая часть суммы. По вертикали – счетчик циклов (слева – для фрактала Фибоначчи, справа – для Люка).

Рис.4. Произведение фракталов Фибоначчи и Люка. Обозначения - как на рис.3

Представленные на рис.3 и 4 изображения с трудом поддаются интерпретации. Изменение начальных условий или секущей временной плоскости приводит к тем же спирально-вихревым структурам с некоторыми внешними отличиями. В этом направлении необходимы дальнейшие исследования. Гипотетически можно предполагать связь рассматриваемой модели с теорией поливихря Бугаева А.Ф. или торсионными полями Шипова Г.И. В этой связи необходимо учитывать следующее обстоятельство. В рамках теории комплексных переменных можно придумать очень много функций, генерирующих спиральные формы в фазовой плоскости. Такова природа этих чисел. В нашем случае нелинейной динамической модели (программа Фибоначчи) комплексные числа появляются естественным образом в рамках обобщения ряда Фибоначчи и формулы Бине, описывающих некоторые свойства чисел натуральных (1, 2, 3, 4, …). Случай в некотором смысле аналогичный квантово-механической теории в физике. Там при решении волнового уравнения Шредингера с необходимостью получаются функции комплексных переменных. Мнимая составляющая, по мнению некоторых эзотериков (например, Шнейдерман А.Г.), отражает непроявленную в нашем пространстве компоненту мироздания.

Фракталы программы Фибоначчи и Хаос.

Для сложных нелинейных динамических систем в рамках синэргетики важное значение имеет понятие точек бифуркации. Сущность явления заключается в том, что при определенных начальных условиях система из детерминированного состояния после некоторого количества циклов развития теряет устойчивость, разрушается и переходит в состояние хаоса. Существуют такие начальные условия и для нашей модели. Это оказались те самые первочисла –φ и 1 . При таких начальных условиях развитие объекта показано на рис.5.

Рис.5. Бифуркационный переход объекта, построенного по программе Фибоначчи. Y (x ) рассчитывалось по ур. (5) с использованием начальных условий:

х 0 = -φ и х 1 = 1.

Для возможно большего охвата количества циклов (по оси Х) значения состояния объекта (по оси Y ) показаны в логарифмическом масштабе. Можно видеть, что точка перехода в состояние динамического хаоса находится при значениях 39-40 циклов. При анализе формулы (5) и полученных результатов было установлено, что поведение системы не изменяется при пропорциональном изменении начальных условий, т.е. для получения точки бифуркации в общем случае: х 0 = -аφ и х 1 = а (где а – любое действительное число, кроме, естественно, тривиального случая а=0). Это иллюстрирует рис.6, где в деталях показан участок бифуркационного перехода.

Рис.6. Область бифуркационного перехода объектов, построенных по программе Фибоначчи.

В качестве критерия состояния объекта использовали модуль, вычисляемый стандартно, как для ряда Фибоначчи (формула (3)). Начальные условия кратны использованным на рис.5, а между собой отличаются в 10 15 (красный цвет – а = 10 7 , синий – а = 10 -8). Можно видеть, что до 36-го цикла объекты развиваются детерминировано, модуль в обоих случаях равен 1/φ (0,61830….). Далее процесс разрушения лавинообразно нарастает и после 39-40 циклов наступает состояние динамического хаоса. Объекты как бы расщепляются и развиваются одновременно в нескольких состояниях (модули – 2, 1, 1/φ, 0). Положение точки бифуркации (39-40 циклов) имеет вероятно фундаментальный смысл в связи с эзотерическими знаниями. Отметим исключительную устойчивость точки бифуркации, т.к. изменение начальных условий на 15 порядков не сместило ее даже на один цикл. Результаты расчетов, представленные на рис.5 и 6, относятся к случаю а > 0. Если а < 0 (например, х 0 = 1 и х 1 = -1/φ), то картина становится зеркальной и точка бифуркации смещается к отрицательным значениям циклов -39-40. Возможно, этот случай представляет модель обратного перехода: «динамический хаос → детерминированная структура».В заключение на рис.7 показан видбифуркационного перехода в динамический хаос с помощью 3-D графики для стороннего «далеко отстоящего» наблюдателя.

Рис.7. Переход «детерминированная структура – динамический хаос» для объекта, строящегося по программе Фибоначчи,

В рамках эзотерических представлений его можно назвать «крестовый разворот». Особенно наглядным это получается при изображении изменений фазового портрета объекта в динамике при использовании возможностей анимации программ Matcad или Matlab .

Заключение.

Предложено понятие «программа Фибоначчи», как обобщение формулы Бине на область всех действительных чисел.
Использование программы Фибоначчи позволяет с помощью рекуррентной формулы моделировать нелинейные динамические системы – спиралевидные фрактальные объекты на множестве комплексных чисел, несущие в своем строении «золотое сечение».
Гипотетический математический алгоритм Мироздания - программа Фибоначчи позволяет объяснить некоторую часть эзотерических представлений.
Существуют определенные начальные условия, при которых объект, созданный по программе Фибоначчи, через 39-40 циклов разрушается и переходит в состояние динамического хаоса.
Человека можно представить целостным фрактальным объектом Мироздания, который находится в непрерывном циклическом развитии в рамках перехода „материальный мир (Ян) – духовное или информационное состояние (Инь)”.

“Дьявол кроется в деталях”

Все слышали, что рынок фрактален (часть подобна целому), что на всех таймфреймах он выглядит одинаково, что он постоянно воссоздает подобные элементы на разных уровнях своей структуры. Обнако с руки Б.Вильямса произошла подмена и резкое сужение непростого понятия “Фрактал” до банальной свечной комбинации.

Процитирую Мандельброта. Он то и ввел в обиход этот термин лет 40 тому назад..

“Фрактал - геометрическая форма, которая может быть разделена на части, каждая из которых - уменьшенная версия целого. В финансах эта концепция - не беспочвенная абстракция, а теоретическая переформулировка практичной рыночной поговорки – а именно, что движения акции или валюты внешне похожи, независимо от масштаба времени и цены. Наблюдатель не может сказать по внешнему виду графика, относятся ли данные к недельным, дневным или же часовым изменениям. Это качество определяет диаграммы как фрактальные кривые и делает доступными многие мощные инструменты из математического и компьютерного анализа”.

Ну, положим, кто-то может по гэпам почувствовать дневные графики, но, по крайней мере, речь шла не о свечной комбинации, а о существенно более емком понятии. А то, “фрактал на покупку, фрактал на продажу”. Все-таки, скажу слово в защиту Билла Вильямса. В последней книге “Торговый Хаос 2” он сетует, что рынки изменились и пытается усилить свою систему. Ему жалко, что он упускает много из ценового движения. И я увидел маленький намек, что он слегка, может, даже не осознавая, сделал маленький шажок в сторону настоящего Фрактала, который скрывался между некоторыми фракталами по Б.В. Между некоторыми точками рынка (хаи и лои, но не все пары) существует невидимая связь, не всегда очевидная, Мандельброт ее чувствовал и пытался ее развить. Один из приемов (он подавал его как шутку) – вырастить из простой затравки график рынка, соблюдая простой алгоритм усложнения через простое подобие (Генератор Мандельброта).

Б.Вильямс этого не чувствовал. Странная у него была команда, математики, программисты. Не понимали они друг друга. Или загрузили себя рутинной работой по подбору параметров скользящих средних. Возможно, надо быть универсалом и строить Вавилонскую башню до какого-то уровня в одиночку. А Хаоса (настоящего, математического) у него, конечно же, тоже не было, как и Фрактала. Есть и еще гипотеза – он прикрывал настоящее знание.

Да, рынок бывает фрактальным. Временами это очевидно. Например, на следующем графике это можно было бы заметить невооруженным, но тренированным, глазом. Здесь, правда, все-таки, с применением техники. Зеленые, розовые и синяя фигуры (все - Фракталы) очень похожи. Можно было бы зеленые фигуры дробить еще глубже, но материала надолго не хватит, свечек ограниченное количество, да, и, из-за дискретности, нарастает относительная погрешность.

На TF(timeframe)=М1.

Довольно типичная для рынка структура (триадная), что на росте-спуске, что в боковике.

Для продвинутых. Теперь уже заметно, что идея генератора у Мандельброта была неплоха (как шутка).

Был бы он еще и трейдером, все бы уже лет 15 изучали его систему трейдинга, а не “машки” или Эллиота. Кстати, Эллиот изучал тренд, педалируя схему 5+3, и много “потерял”, в частности – боковик. А вполне мог бы ограничиться числом 3. А, так, Фрактал многое поглотил, включая волны Эллиота.

Заметно, что некоторые структуры начинают ломаться. На TF=М15 кто-то уже сказал бы: “пила, тухлый боковик”. А на самом деле боковик при соответствующей детализации просто прекрасен, надо просто перейти на более мелкий TF.

На TF=D структура просто была бы совершенно не видна, вся эта красота закрывалась бы одной дневной свечкой.

Рынок дискретен. Поток элементарных сделок, идущих то чаще, то реже. Снимаю шляпу перед теми, кто работает на тиковом уровне – они пытаются работать с первоисточником. Идеально, если у вас есть HFT-робот, находящийся непосредственно на бирже. Но большинство из нас торгуют дома или на работе. Между нами и биржей – брокер и телекоммуникационная среда. Информация о заявках и сделках, обычно накопленная в пакетах в некотором количестве (как бы, минисвечка или минибар), доходит до нас с некоторым опозданием, примерно на десятые доли секунды или еще медленнее. Да, еще, может, и разными логическими каналами в разные таблицы торгового терминала. Дискретность пакета и задержки – это реалии.

А потом начинается ужасное - торговый терминал режет эту еще слегка искаженную последовательность на свечки-бары по желанию пользователя, как колбасу, обычно ровными порциями, на минутной, часовой, дневной и т.д. основе. Детали теряются, и чем выше TF, тем больше их теряется. Конкретное время, когда рынок достиг своего экстремума, спряталось внутри интервала свечки. Да, еще и эта условная нарезка по временным интервалам. Есть же и другие виды графиков. Одно время я исследовал эквивольюмные графики, на которых свечки имеют ширину, пропорциональную объему. Этап был проходной, но полезный.

Еще один дефект нарезки рыночного трафика на свечки-бары. Экстремумы (High-Low) абсолютны, а вот Open-Close – относительны. Сместите часовой график минут на 5, экстремумы еще могут остаться на месте в той же часовой свечке и не изменить своего значения, а у Open-Close шансов очень мало.

Поэтому, для меня естественным было бы работать на минимально допустимом TF (по техническим или физиологическим возможностям). Это качественно, по степени детализации и близости к тиковому уровню.

Многие задаются вопросом, на каком TF надо работать? Попробуем оценить количественно, пусть грубо, что еще, кроме деталей, теряется при переходе на другой, более высокий таймфрейм.

В середине прошлого века был обнаружен парадокс береговой линии. Разные измерения одной и той же границы или береговой линии давали сильно отличающиеся результаты, в зависимости от того какой единицей она измерялась. Через некоторое время Бенуа Мандельброт разработал новую область математики, фрактальную геометрию, для описания именно таких объектов в природе. И рынок по этой же причине попал в поле зрения Мандельброта.

Прикинем сумму высот свечек за день, например, для fRTS, на TF=D, TF=H1 и TF=M1. Может, кто-то думает, что они совпадают (объемы – да, совпадают)? Можно, например, воспользоваться индикатором ATR (Average True Range) или, грубо, можно ориентироваться на корень квадратный из соотношения таймфреймов. Распределением объемов и высот свечек я тоже занимался и даже сделал полезный индикатор.

Для TF=D сумма высот свечек в заурядный день это 2-3 тысячи пунктов, для TF=H1 это 8-10 тысяч пунктов, а для TF=M1 – 60-80 тысяч (если правильно запомнил, то 16.12.2014 было 484 тысячи). Это ориентир для нашей потенциальной прибыли (выбрать все свечки по всей высоте). Получить прибыль в 7 раз больше при переходе с H1 на M1 – нельзя игнорировать это обстоятельство (правда, объем работы увеличится в 60 раз.). Это я прояснил для себя еще до того, как выбрал брокера. Но физиологически я не мог работать на TF ниже M15. Сейчас, вооруженный до зубов, считаю TF=M1 медленным.

Оценивал TF=1sec, искусственно строя секундные свечки для fRTS и исследуя их в Excel. На этом таймфрейме рынок выглядит так же, как и на других. Алгоритмы выдержали. Вот и определился тот таймфрейм, на котором надо работать дома (роботом) с учетом задержек. Потенциально увеличение прибыли еще где-то в 7 раз.

Я не люблю использовать термин “таймфрейм”. У меня он фиксирован – M1 (предельная детализация по свечкам). Мне естественнее говорить “торговый горизонт”. У меня он редко уходит за 2-3 дня. Могу для поддержания разговора или если надо посмотреть что-то. Мог бы работать и на H1, и на D1 (система позволяет), но арифметику я знаю хорошо.

Разумеется, все это справедливо для ликвидных инструментов. Проверял работу системы на акциях ТГК-2, там 90% всех минуток проходили без сделок, были дни, когда до обеда сделок совсем не было. Работая на TF=M1 я застрял в позе на месяц, тогда, как на fRTS среднее время нахождения в позе – 10мин.

А если вы ворочаете миллиардами, то для вас нужен отдельный пост. Как продать или купить большой пакет акций, не уронив рынок и не взвинтив его в космос? Тоже есть ответ.

Вы не можете перейти на споте на минутки, потому, что комиссия превысит прибыль? Переходите на ФОРТС, там комиссия просто символическая (не считая других достоинств).

Ваша система покупает летом, а продает зимой или работает по фазам луны? Извините, ваша система не масштабируется, преимущества фрактальности не для вас.

В вашей системе зафиксированы конкретные значения параметров каких-то индикаторов и она плохо работает на других TF? Тоже, извините.

Вы физиологически не успеваете следить за своими индикаторами и выполнять нужные построения? Это проблема ваша или вашей системы. Автоматизируйте.

Потенциально, масштабируемые системы могут воспользоваться этим очевидным свойством фрактальности, особенно при автоматизации.

Математики спокойно занимались фрактальными объектами задолго до Мандельброта. Так часто бывает. Но как только становится очевидным прикладной характер, идет взрывоподобное развитие. Материаловедение, технология Stealth, фрактальные антенны – много куда проникла фрактальность. Теперь и рынок может взорваться (в разных смыслах).

С несколькими Фракталами я познакомился в средних классах, еще лет 10-15 оставалось до внедрения в массы этого термина. О кроликах Фибоначчи я узнал еще раньше, все из тех же научно-популярных книжек и брошюрок.

Треугольник Серпинского.

Кривая Дракона (опреденно есть у Гарднера, но, уверен, встречал и раньше).

Генератор Мандельброта. Идея, как в кривой Дракона. Уже ближе к рыночным графикам.

О курьезах. Я с детства, оказывается, знал что-то о Фракталах и Фибоначчи. О генераторе Мандельброта я узнал, когда уже писал этот пост. Фамилию Мандельброт мне подсказали, когда я уже озвучил свои первые результаты. Я никогда не занимался ни чистой математикой, ни прикладной. Но, думаю, мехмат с красивой и строгой математикой сидит во мне прочно. Я не помню, когда я узнал о проблеме береговой линии, но фрактальность рынка принял совершенно естественно.

Говорят, что Фракталы хорошо описывают природу, но не объясняют ее. В части рынка хорошие объяснения его сути у меня определенно есть. Хотя, формально это уже, как бы, лишнее.

Я стал подбирать математический аппарат, на базе которого можно было развивать некоторые мысли и наблюдения.

Экспонента Херста. Временные ряды. Персистентность. Антиперсистентность. Прошел исключительно поверхностно. Почувствовал некоторую инерционность, усредненность и закладываемое отставание. Требовалось большое количество данных. Использование стандартных отклонений отталкивало. Мне больше подходила динамика, ведь рынок очень динамичен. Да и слишком много народа занималось временными рядами.

Теория групп – тогда было очень рано, ее время еще не пришло, но скоро может наступить. Трейдеры, специалисты по теории групп, готовьтесь занять нишу. Можно попробовать навести порядок во фрактальных структурах.

Фрактальная геометрия – очень легко, по простым алгоритмам, получаются красивые сложные статические фигуры. Смоделировать рынок из простых затравок, типа генератора Мандельброта, было очень частной задачей. Было бы этими моделями охвачено все многообразие рынка – неизвестно.

Но была одна необычная математическая дисциплина. Она была несколько не в ладах с классической наукой, в которой какие-то идеи что-то предсказывают, а предсказания сверяют с реальными результатами. Теория Хаоса занималась непредсказуемыми системами.

Теория Хаоса (теория нелинейных динамических систем, с непостоянным и непериодическим изменением траектории) имеет отношение к фрактальными системам и к рынку. Только не Билла Вильямса, а математическая (вот, ведь, человек – использовал два прекрасных термина совершенно не по назначению). Под хаосом в быту вообще понимают полный беспорядок, в то время как Хаос - это особая, изысканная форма порядка.

Представьте себе автомобиль, который едет равномерно-прямолинейно по прямой. Вы всегда знаете, где он был или будет находиться в любой момент времени. Можно заменить прямую на синусоиду, а равномерное движение на равноускоренное – принципиально ничего не меняется. Полная предопределенность.

Другая крайность – бросание монетки. Полная непредсказуемость результата.

Хаос занимает промежуточное положение. Он выглядит случайным, беспорядочным, однако в нем есть закономерности, но они обнаруживаются не сразу (“Видишь суслика? Нет. И я не вижу. А он есть.” (ДМБ)). Но, в то же время, при наличии закономерностей, результат движения является непредсказуемым. Вот такое интересное сочетание.

Первый вывод Теории Хаоса – будущее точно предсказать невозможно. Много раз встречал ситуации, когда до целевой кривой оставалось буквально полсвечки, но рынок откатывался и закономерно выходил на целевую только на следующий день и совсем на другом уровне. Поэтому прогнозами не занимаюсь – теория не велит.

При всей непредсказуемости траектории движения существуют рамки, пределы, которые это движение ограничивают. Эти статичные рамки и образуют Фрактал, но только по завершении движения. То есть, предельное положение хаотической системы (динамического явления) и есть Фрактал (статическое явление). Тот самый Фрактал из фрактальной геометрии. В процессе движения прообраз фрактала тоже меняется, уточняется, приближается к законченной форме, с возникновением промежуточных финишей. Дополнительно, результат существенно зависит от начальных данных и от факторов воздействия во время движения (для рынков, например, от новостей или действий трейдеров).

Некоторая аналогия (аналогия – это не доказательство). Зарядили пушку (порох, ядро), установили угол (прицелились) и выстрелили. Место пушки, количество пороха, прицел – начальные условия. Баллистик скажет – полетит по параболе. При некоторых условиях – правдоподобно. При других – вполне может выйти и на эллиптическую орбиту, и на гиперболическую. А в микромире и вовсе другие закономерности. В рынке фрактальные свойства тоже могут иметь свой диапазон.

И летит ядро, пока не встретит препятствие. А здесь уже рельеф местности играет роль, гора ли на пути или ущелье, а, при правильных начальных условиях – какая-нибудь точка на крепостной стене. Встреча ядра с препятствием неизбежна (закономерность) и зависит от начальных условий и текущего рельефа (+ гравитационные аномалии), а каким рельеф будет – мы еще не знаем, поэтому и не знаем, где и когда ядро встретит рельеф (непредсказуемость).

У нас так же. Только траектория (целевая кривая) специфическая. И начальные условия важны, еще и профиль графика корректирует траекторию.

Как при таких установках найти что-то закономерное?

Есть смягчающие ситуацию факторы. Хаотические системы – с обратной связью, последующие значения зависят от предыдущих (память). В хаотических системах есть много точек равновесия.

Взгляните еще раз на вышеприведенные графики, теперь уже на динамику.

Мне понравился второй вывод Теории Хаоса – достоверность прогнозов со временем быстро падает. Этот вывод является существенным ограничением для применимости фундаментального анализа, оперирующего, как правило, именно долгосрочными категориями. Поэтому для меня естественно работать накоротке, “прямой наводкой”, на не очень больших торговых горизонтах (обычно не более 1-2 дня на минутках). Есть еще очень важное обстоятельство. К моему удовлетворению, рыночная фрактальность дала очень мощную возможность повысить точность (что-то вроде самофокусировки лазерного луча).

Прекрасно подходила Теория Хаоса под мои задачи, но осваивать ее я не собирался.

Теория Хаоса сказала мне, что в хаотичных системах есть странные аттракторы (точки, кривые, фигуры), к которым притягиваются элементы системы. В частности, странные аттракторы образуют определенные рамки движения. И есть у них особенность - они существенно зависят от точки приложения (более широко – от начальных условий).

И стал я искать странные аттракторы. Мне просто деваться было некуда, все было так хорошо объяснено. Я нашел их с десяток. Один из странных аттракторов оказался фигурой - Фракталом. Есть в его формуле одна интересная деталь, я ее обнаружил когда решил основное уравнение - деталь называется «среднее гармоническое». Для математика это очень ценно. А Фрактал получился и обобщением основной гармонической модели AB=CD, и обобщением Генератора Мандельброта, похоже, что и Волны Эллиота может закрыть. Одновременно целевая и коррекционные кривые обобщили дискретность расширений и коррекций Фибоначчи до непрерывности. И еще какие-то мелочи.

Странными путями иногда доходила до меня информация, дающая мне ценные импульсы.
В выходные на даче как-то застал по ТВ самый конец боевика-детектива, где играли У.Снайпс и Дж.Стэтэм.
Один из них говорит (не дословно): ”Cобытия, поначалу кажущиеся случайными, со временем могут стать закономерностью. Называется Теория Хаocа".

Посмотрел в домашней коллекции с другим переводом: «Один случайный поступок тянет за собой другой, другой следующий, в конце возникает закономерность. Это Теория Хаоca».
Фильм назывался ”Хаос".

Какие ассоциации у нормального человека должны были возникнуть при упоминании термина “подобие”? Правильно, подобные треугольники.

Но, не только. Чем не суперпозиция (в собранном виде)?

Фракталы не обязаны иметь красивую форму, как в триадной структуре. Вот форма, напоминающая треугольники.

P.S. Кто прочитает предпоследний абзац раздела из книги Э.Наймана (“Путь к финансовой свободе. Глава 6. В поисках Грааля. 6.2.Теория Хаоса на службе у трейдера”) о проблемах совместимости Теории Хаоса с классической наукой, поймет, что я только из духа противоречия должен был выбрать Теорию Хаоса.

Э.Найман советует не спешить с применением знаний о хаосе. А я и не спешил.

А еще он подтверждает, что это самое перспективное современное направление для прикладных исследований финансовых рынков .

И я тоже это подтверждаю.

Теория хаоса в последнее время является одним из самых модных подходов к исследованию рынка. К сожалению, точного математического определения понятия хаос пока не существует. Сейчас зачастую хаос определяют как крайнюю непредсказуемость постоянного нелинейного и нерегулярного сложного движения, возникающую в динамической системе.

ХАОС НЕ СЛУЧАЕН

Следует отметить, что хаос не случаен, несмотря на свойство непредсказуемости. Более того, хаос динамически детерминирован (определен). На первый взгляд непредсказуемость граничит со случайностью - ведь мы, как правило, не можем предсказать как раз случайные явления.

И если относиться к рынку как к случайным блужданиям, то это как раз тот самый случай. Однако хаос не случаен, он подчиняется своим закономерностям. Согласно теории хаоса, если вы говорите о хаотичном движении цены, то вы должны иметь ввиду не случайное движение цены, а другое, особенно упорядоченное движение. Если динамика рынка хаотична, то она не случайна, хотя и по-прежнему непредсказуема.

Непредсказуемость хаоса

Непредсказуемость хаоса объясняется в основном существенной зависимостью от начальных условий. Такая зависимость указывает на то, что даже самые малые ошибки при измерении параметров исследуемого объекта могут привести к абсолютно неверным предсказаниям.

Эти ошибки могут возникать вследствие элементарного незнания всех начальных условий. Что-то обязательно ускользнет от нашего внимания, а значит, уже в самой постановке задачи будет заложена внутренняя ошибка, которая приведет к существенным погрешностям в предсказаниях.

"Эффект бабочки"

Применительно к невозможности делать долгосрочные прогнозы погоды существенную зависимость от начальных условий иногда называют "эффектом бабочки". "Эффект бабочки" указывает на существование вероятности того, что взмах крыла бабочки в Бразилии приведет к появлению торнадо в Техасе.

Дополнительные неточности в результат исследований и расчетов могут вносить самые на первый взгляд незаметные факторы воздействия на систему, которые появляются в период ее существования с начального момента до появления фактического и окончательного результата. При этом факторы воздействия могут быть как экзогенные (внешние), так и эндогенные (внутренние).

Ярким примером хаотического поведения является движение бильярдного шара. Если вы когда-либо играли в бильярд, то знаете, что от начальной точности удара, его силы, положения кия относительно шара, оценка месторасположения шара, по которому наносится удар, а также расположения других шаров, находящихся на столе, зависит конечный результат. Малейшая неточность в одном из этих факторов приводит к самым непредсказуемым последствиям - шар может покатиться совсем не туда, куда ожидал бильярдист. Более того, даже если бильярдист все сделал правильно, попробуйте предсказать движения шара после пяти-шести столкновений.

Рассмотрим еще один пример влияния начальных условий на конечный результат. Представим себе, например, камень на вершине горы. Стоит его чуть-чуть подтолкнуть, и он покатится вниз до самого подножия горы. Понятно, что совсем малое изменение силы толчка и его направления может привести к очень значительному изменению места остановки камня у подножия. Есть, правда, одна очень существенная разница между примером с камнем и хаотической системой.

В первом факторы воздействия на камень во время его падения с горы (ветер, препятствия, изменения внутренней структуры вследствие столкновений и т.п.) уже не оказывают сильного воздействия на конечный результат по сравнению с начальными условиями. В хаотических системах малые изменения оказывают значительное воздействие на результат не только в начальных условиях, но и прочих факторах.

Один из главных выводов теории хаоса, таким образом, заключается в следующем - будущее предсказать невозможно, так как всегда будут ошибки измерения, порожденные в том числе незнанием всех факторов и условий.

То же самое по-простому - малые изменения и/или ошибки могут порождать большие последствия.

Рисунок 1. Существенная зависимость результата от начальных условий и факторов воздействия

Еще одним из основных свойств хаоса является экспоненциальное накопление ошибки. Согласно квантовой механике начальные условия всегда неопределенны, а согласно теории хаоса - эти неопределенности будут быстро прирастать и превысят допустимые пределы предсказуемости.
Второй вывод теории хаоса - достоверность прогнозов со временем быстро падает.

Данный вывод является существенным ограничением для применимости фундаментального анализа, оперирующего, как правило, именно долгосрочными категориями.

Рисунок 2. Экспоненциальное снижение достоверности прогнозов

Обычно говорят, что хаос является более высокой формой порядка, однако более правильно считать хаос другой формой порядка - с неизбежностью в любой динамической системе за порядком в обычном его понимании следует хаос, а за хаосом порядок. Если мы определим хаос как беспорядок, то в таком беспорядке мы обязательно сможем увидеть свою, особенную форму порядка. Например, дым от сигарет сначала поднимающийся в виде упорядоченного столба под влиянием внешней среды принимает все более причудливые очертания, а его движения становятся хаотичными.

Еще один пример хаотичности в природе - лист с любого дерева. Можно утверждать, что вы найдете много похожих листьев, например дуба, однако ни одной пары одинаковых листьев. Разница предопределена температурой, ветром, влажностью и многими другими внешними факторами, кроме чисто внутренних причин (например, генетической разницей).

Движение от порядка к хаосу и обратно, по всей видимости, является сущностью вселенной, какие бы проявления ее мы не изучали. Даже в человеческом мозгу одновременно присутствует упорядоченное и хаотическое начала. Первое соответствует левому полушарию мозга, а второе - правому. Левое полушарие отвечает сознательное поведение человека, за выработку линейных правил и стратегий в поведении человека, где четко определяется "если…, то…". В правом же полушарии царит нелинейность и хаотичность. Интуиция является одним из проявлений правого полушария мозга.

Теория хаоса изучает порядок хаотической системы, которая выглядит случайной, беспорядочной. При этом теория хаоса помогает построить модель такой системы, не ставя задачу точного предсказания поведения хаотической системы в будущем.

Первые элементы теории хаоса появились еще в XIX веке, однако подлинное научное развитие эта теория получила во второй половине XX века, вместе с работами Эдварда Лоренца (Edward Lorenz) из Массачусетского технологического института и франко-американского математика Бенуа Б. Мандельброта (Benoit B. Mandelbrot).

Эдвард Лоренц в свое время (начало 60-х годов XX века, работа опубликована в 1963 году) рассматривал, в чем возникает трудность при прогнозировании погоды.

До работы Лоренца в мире науки господствовало два мнения относительно возможности точного прогнозирования погоды на бесконечно длительный срок.

Первый подход сформулировал еще в 1776 году французский математик Пьер Симон Лаплас. Лаплас заявил, что "…если мы представим себе разум, который в данное мгновение постиг все связи между объектами во Вселенной, то он сможет установить соответствующее положение, движения и общие воздействия всех этих объектов в любое время в прошлом или в будущем" . Этот его подход был очень похож на известные слова Архимеда: "Дайте мне точку опоры, и я переверну весь мир".

Таким образом, Лаплас и его сторонники говорили, что для точного прогнозирования погоды необходимо только собрать больше информации обо всех частицах во Вселенной, их местоположении, скорости, массе, направлении движения, ускорении и т.п. Лаплас думал, чем больше человек будет знать, тем точнее будет его прогноз относительно будущего.

Второй подход к возможности прогнозирования погоды раньше всех наиболее четко сформулировал другой французский математик, Жюль Анри Пуанкаре. В 1903 году он сказал: "Если бы мы точно знали законы природы и положение Вселенной в начальный момент, мы могли бы точно предсказать положение той же Вселенной в последующий момент. Но даже если бы законы природы открыли нам все свои тайны, мы и тогда могли бы знать начальное положение только приближенно. Если бы это позволило нам предсказать последующее положение с тем же приближением, это было бы все, что нам требуется, и мы могли бы сказать, что явление было предсказано, что оно управляется законами. Но это не всегда так; может случиться, что малые различия в начальных условиях вызовут очень большие различия в конечном явлении. Малая ошибка в первых породит огромную ошибку в последнем. Предсказание становится невозможным, и мы имеем дело с явлением, которое развивается по воле случая".

В этих словах Пуанкаре мы находим постулат теории хаоса о зависимости от начальных условий. Последующее развитие науки, особенно квантовой механики, опровергло детерминизм Лапласа. В 1927 году немецкий физик Вернер Гейзенберг открыл и сформулировал принцип неопределенности. Этот принцип объясняет, почему некоторые случайные явления не подчиняются лапласовому детерминизму. Гейзенберг показал принцип неопределенности на примере радиоактивного распада ядра. Так, из-за очень малых размеров ядра невозможно знать все процессы, происходящие внутри него. Поэтому, сколько бы информации мы не собирали о ядре, точно предсказать, когда это ядро распадется невозможно.

Какими же инструментами располагает теория хаоса. В первую очередь это аттракторы и фракталы.

Аттрактор (от англ. to attract - притягивать) - геометрическая структура, характеризующая поведение в фазовом пространстве по прошествии длительного времени.

Здесь возникает необходимость определить понятие фазового пространства. Итак, фазовое пространство - это абстрактное пространство, координатами которого являются степени свободы системы. Например, у движения маятника две степени свободы. Это движение полностью определено начальной скоростью маятника и положением.

Если движению маятника не оказывается сопротивления, то фазовым пространством будет замкнутая кривая. В реальности на Земле на движение маятника влияет сила трения. В этом случае фазовым пространством будет спираль.

Рисунок 3. Движение маятника как пример фазового пространства

По простому, аттрактор - это то, к чему стремится прийти система, к чему она притягивается.

Самым простым типом аттрактора является точка. Такой аттрактор характерен для маятника при наличии трения. Независимо от начальной скорости и положения, такой маятник всегда придет в состояние покоя, т.е. в точку.
Следующим типом аттрактора является предельный цикл, который имеет вид замкнутой кривой линии. Примером такого аттрактора является маятник, на который не влияет сила трения. Еще одним примером предельного цикла является биение сердца. Частота биения может снижаться и возрастать, однако она всегда стремится к своему аттрактору, своей замкнутой кривой.
Третий тип аттрактора - тор. На рисунке 4. тор показан в верхнем правом углу.

Рисунок 4. Основные типы аттракторов. Вверху показаны три предсказуемых, простых аттрактора. Внизу три хаотических аттрактора.

Несмотря на сложность поведения хаотических аттракторов, иногда называемых странными аттракторами, знание фазового пространства позволяет представить поведение системы в геометрической форме и соответственно предсказывать его.

И хотя нахождение системы в конкретный момент времени в конкретной точке фазового пространства практически невозможно, область нахождения объекта и его стремление к аттрактору предсказуемы.

Первым хаотическим аттрактором стал аттрактора Лоренца. На рисунке 3.7. он показан в левом нижнем углу.

Рисунок 5. Хаотический аттрактор Лоренца

Аттрактор Лоренца рассчитан на основе всего трех степеней свободы - три обыкновенных дифференциальных уравнения, три константы и три начальных условия. Однако, несмотря на свою простоту, система Лоренца ведет себя псевдослучайным (хаотическим) образом.

Смоделировав свою систему на компьютере, Лоренц выявил причину ее хаотического поведения - разницу в начальных условиях. Даже микроскопическое отклонение двух систем в самом начале в процессе эволюции приводило к экспоненциальному накоплению ошибок и соответственно их стохастическому расхождению.

Вместе с тем, любой аттрактор имеет граничные размеры, поэтому экспоненциальная расходимость двух траекторий разных систем не может продолжаться бесконечно. Рано или поздно орбиты вновь сойдутся и пройдут рядом друг с другом или даже совпадут, хотя последнее очень маловероятно. Кстати, совпадение траекторий является правилом поведения простых предсказуемых аттракторов.

Сходимость-расходимость (говорят также, складывание и вытягивание соответственно) хаотического аттрактора систематически устраняет начальную информацию и заменяет ее новой. При схождении траектории сближаются и начинает проявляться эффект близорукости - возрастает неопределенность крупномасштабной информации. При расхождении траекторий наоборот, они расходятся и проявляется эффект дальнозоркости, когда возрастает неопределенность мелкомасштабной информации.

В результате постоянной сходимости-расходимости хаотичного аттрактора неопределенность стремительно нарастает, что с каждым моментом времени лишает нас возможности делать точные прогнозы. То, чем так гордится наука - способностью устанавливать связи между причинами и следствиями - в хаотических системах невозможно. Причинно-следственной связи между прошлым и будущем в хаосе нет.

Здесь же необходимо отметить, что скорость схождения-расхождения является мерой хаоса, т.е. численным выражением того, насколько система хаотична. Другой статистической мерой хаоса служит размерность аттрактора.

Таким образом, можно отметить, что основным свойством хаотических аттракторов является сходимость-расходимость траекторий разных систем, которые случайным образом постепенно и бесконечно перемешиваются

Здесь проявляется пересечение фрактальной геометрии и теории хаоса. И, хотя одним из инструментов теории хаоса является фрактальная геометрия , фрактал - это противоположность хаоса.

Главное различие между хаосом и фракталом заключается в том, что первый является динамическим явлением, а фрактал статическим. Под динамическим свойством хаоса понимается непостоянное и непериодическое изменение траекторий.

ФРАКТАЛ

Фрактал - это геометрическая фигура, определенная часть которой повторяется снова и снова, отсюда проявляется одно из свойств фрактала - самоподобие.

Другое свойство фрактала - дробность. Дробность фрактала является математическим отражением меры неправильности фрактала.

Фактически все, что кажется случайным и неправильным может быть фракталом, например, облака, деревья, изгибы рек, биения сердца, популяции и миграции животных или языки пламени.

Рисунок 6. Фрактал "ковер Серпинского"

Данный фрактал получается путем проведения ряда итераций. Итерация (от лат. iteratio - повторение) - повторное применение какой-либо математической операции.

Рисунок 7. Построение ковра Серпинского

Хаотический аттрактор является фракталом. Почему? В странном аттракторе, также как и во фрактале по мере увеличения выявляется все больше деталей, т.е. срабатывает принцип самоподобия. Как бы мы не изменяли размер аттрактора, он всегда останется пропорционально одинаковым.

В техническом анализе типичным примером фрактала являются волны Эллиота, где также работает принцип самоподобия.

Первым наиболее известным и авторитетным ученым, исследовавшим фракталы, был Бенуа Мандельброт. В середине 60-х годов XX века разработал фрактальную геометрию или, как он ее еще назвал - геометрию природы. Об этом Мандельброт написал свой известный труд "Фрактальная геометрия природы" (The Fractal Geometry of Nature) . Многие называют Мандельброта отцом фракталов, т.к. он первым начал использовать его применительно к анализу нечетких, неправильных форм.

Дополнительная идея, заложенная во фрактальности, заключается в нецелых измерениях. Мы обычно говорим об одномерном, двумерном, трехмерном и т.д. целочисленном мире. Однако могут существовать и нецелые измерения, например, 2.72. Такие измерения Мандельброт называет фрактальными измерениями.

Логика существования нецелых измерений очень простая. Так, в природе вряд ли найдется идеальный шар или куб, следовательно, 3-мерное измерение этого реального шара или куба невозможно и для описания таких объектов должны существовать другие измерения.

Вот для измерения таких неправильных, фрактальных фигур и было введено понятие фрактальное измерение. Скомкайте, например, лист бумаги в комок. С точки зрения классической евклидовой геометрии новообразованный объект будет являться трехмерным шаром. Однако в действительности это по-прежнему всего лишь двумерный лист бумаги, пусть и скомканный в подобие шара. Отсюда можно предположить, что новый объект будет иметь измерение больше 2-х, но меньше 3-х. Это плохо укладывается в евклидовую геометрию, но хорошо может быть описано с помощью фрактальной геометрии, которая будет утверждать, что новый объект будет находиться во фрактальном измерении, приблизительно равном 2.5, т.е. иметь фрактальную размерность около 2.5.

Детерминистские фракталы

Различают детерминистские фракталы, примером которых является ковер Серпинского, и сложные фракталы. При построении первых не нужны формулы или уравнения. Достаточно взять лист бумаги и провести несколько итераций над какой-нибудь фигурой. Сложным фракталам присуща бесконечная сложность, хотя и генерируются простой формулой.

Классическим примером сложного фрактала является множество

Мандельброта, получаемое из простой формулы Zn+1=Zna+C, где Z и C - комплексные числа и а - положительное число. На рисунке 8 мы видим фрактал 2-й степени, где а = 2.

Рисунок 8. Множество Мандельброта

К хаосу системы могут переходить разными путями. Среди последних выделяют бифуркации, которые изучает теория бифуркаций.

Бифуркация (от лат. bifurcus - раздвоенный) представляет собой процесс качественного перехода от состояния равновесия к хаосу через последовательное очень малое изменение (например, удвоение Фейгенбаума при бифуркации удвоения) периодических точек.

Обязательно необходимо отметить, что происходит качественное изменение свойств системы, т.н. катастрофический скачок. Момент скачка (раздвоения при бифуркации удвоения) происходит в точке бифуркации.

Хаос может возникнуть через бифуркацию, что показал Митчел Фейгенбаум (Feigenbaum). При создании собственной теории о фракталах Фейгенбаум, в основном, анализировал логистическое уравнение Xn+1=CXn - С(Хn)2, где С - внешний параметр, откуда вывел, что при некоторых ограничениях во всех подобных уравнениях происходит переход от равновесного состояния к хаосу.

Ниже рассмотрен классический биологический пример этого уравнения.

Например, изолированно живет популяция особей нормированной численностью Xn. Через год появляется потомство численностью Xn+1. Рост популяции описывается первым членом правой части уравнения (СХn), где коэффициент С определяет скорость роста и является определяющим параметром. Убыль животных (за счет перенаселенности, недостатка пищи и т.п.) определяется вторым, нелинейным членом (С(Хn)2).

Результатом расчетов являются следующие выводы:

при С < 1 популяция с ростом n вымирает;
в области 1 < С < 3 численность популяции приближается к постоянному значению Х0 = 1 - 1/С, что является областью стационарных, фиксированных решений. При значении C = 3 точка бифуркации становится отталкивающей фиксированной точкой. С этого момента функция уже никогда не сходится к одной точке. До этого точка былапритягивающая фиксированная ;
в диапазоне 3 < С < 3.57 начинают появляться бифуркации и разветвление каждой кривой на две. Здесь функция (численность популяции) колеблется между двумя значениями, лежащими на этих ветвях. Сначала популяция резко возрастает, на следующий год возникает перенаселенность и через год численность снова уменьшается;
при C > 3.57 происходит перекрывание областей различных решений (они как бы закрашиваются) и поведение системы становится хаотическим.

Отсюда вывод - заключительным состоянием эволюционирующих физических систем является состояние динамического хаоса.

Зависимость численности популяции от параметра С приведена на следующем рисунке.

Рисунок 9. Переход к хаосу через бифуркации, начальная стадия уравнения Xn+1=CXn - С(Хn)2

Динамические переменные Xn принимают значения, которые сильно зависят от начальных условий. При проведенных на компьютере расчетах даже для очень близких начальных значений С итоговые значения могут резко отличаться. Более того, расчеты становятся некорректными, так как начинают зависеть от случайных процессов в самом компьютере (скачки напряжения и т.п.).

Таким образом, состояние системы в момент бифуркации является крайне неустойчивым и бесконечно малое воздействие может привести к выбору дальнейшего пути движения, а это, как мы уже знаем, является главным признаком хаотической системы (существенная зависимость от начальных условий).

Фейгенбаум установил универсальные закономерности перехода к динамическому хаосу при удвоении периода, которые были экспериментально подтверждены для широкого класса механических, гидродинамических, химических и других систем. Результатом исследований Фейгенбаум стало т.н. "дерево Фейгенбаума".

Рисунок 10. Дерево Фейгенбаума (расчет на основе немного измененной логистической формулы)

Что же такое бифуркации в обыденности, по простому. Как мы знаем из определения, бифуркации возникают при переходе системы от состояния видимой стабильности и равновесия к хаосу.

Примерами таких переходов являются дым, вода и многие другие самые обычные природные явления. Так, поднимающийся вверх дым сначала выглядит как упорядоченный столб. Однако через некоторое время он начинает претерпевать изменения, которые сначала кажутся упорядоченными, однако затем становятся хаотически непредсказуемыми.

Фактически первый переход от стабильности к некоторой форме видимой упорядоченности, но уже изменчивости, происходит в первой точке бифуркации. Далее количество бифуркаций увеличивается, достигая огромных величин. С каждой бифуркацией функция турбулентности дыма приближается к хаосу.

С помощью теории бифуркаций можно предсказать характер движения, возникающего при переходе системы в качественно иное состояние, а также область существования системы и оценить ее устойчивость.

К сожалению, само существование теории хаоса трудно совместимо с классической наукой. Обычно научные идеи проверяются на основании предсказаний и их сверки с реальными результатами. Однако, как мы уже знаем, хаос непредсказуем, когда изучаешь хаотическую систему, то можно прогнозировать только модель ее поведения.

Поэтому с помощью хаоса не только нельзя построить точный прогноз, но и, соответственно, проверить его. Однако это не должно говорить о неверности теории хаоса, подтвержденной как в математических расчетах, так и в жизни.

На сейчас еще не существует математически точного аппарата применения теории хаоса для исследования рыночных цен, поэтому спешить с применением знаний о хаосе нельзя. Вместе с тем, это действительно самое перспективное современное направление математики с точки зрения прикладных исследований финансовых рынков.